用于轴和机械设备的动平衡装置 Balanset-1A 售价 1751 欧元。
转子是一个围绕某个轴线旋转的主体,由其轴承表面固定在支架上。转子的轴承表面通过滚动轴承或滑动轴承将负载传递到支架上。轴承表面是耳轴的表面或替代耳轴的表面。
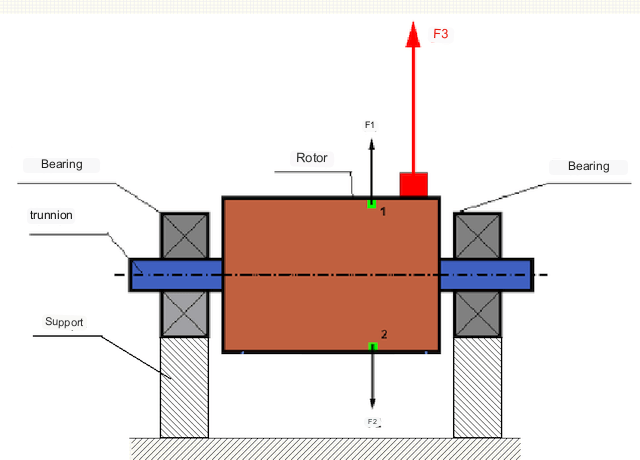
图 1 转子和作用在转子上的离心力
在完全平衡的转子中,其质量围绕旋转轴对称分布,即转子的任何元件都可以与位于旋转轴对称位置的另一元件匹配。在平衡转子中,作用在任何转子元件上的离心力都会被作用在对称元件上的离心力所平衡。例如,离心力 F1 和 F2 的大小相等,方向相反,分别作用在元件 1 和 2 上(图 1 中标注为绿色)。所有对称转子元件都是如此,因此作用在转子上的总离心力为 0,转子是平衡的。
但是,如果转子的对称性被破坏(图 1 中红色标记为不对称元件),那么不平衡离心力 F3 就会作用在转子上。旋转时,该力随转子的旋转而改变方向。该力产生的动载荷传递到轴承上,导致轴承加速磨损。
此外,在这种方向力变化的影响下,固定转子的支架和地基会发生周期性变形,即产生振动。为了消除转子的不平衡和随之而来的振动,必须安装平衡块来恢复转子的对称性。
转子平衡是通过增加平衡质量来纠正不平衡的操作。
平衡的任务是找到一个或多个平衡质量的大小和位置(角度)。
转子类型和不平衡类型。
考虑到转子材料的强度和作用在转子上的离心力大小,转子可分为两种--刚性转子和柔性转子。
在工作模式下,刚性转子在离心力作用下的变形很小,因此可以忽略这种变形对计算的影响。
挠性转子的变形已不容忽视。与刚性转子的平衡问题相比,挠性转子的变形使平衡问题的解决变得复杂,需要应用其他数学模型。需要注意的是,同一转子在低速时可能表现为刚性,而在高速时则表现为挠性。在下文中,我们将只考虑刚性转子的平衡问题。
根据不平衡质量沿转子长度方向的分布,可将不平衡分为两种类型--静态和动态(瞬间)。因此,转子平衡分为静态平衡和动态平衡。静态转子不平衡在转子不旋转的情况下发生,即在静态情况下,转子在重力作用下反转,"重点 "向下。静态不平衡转子的示例如图 2 所示
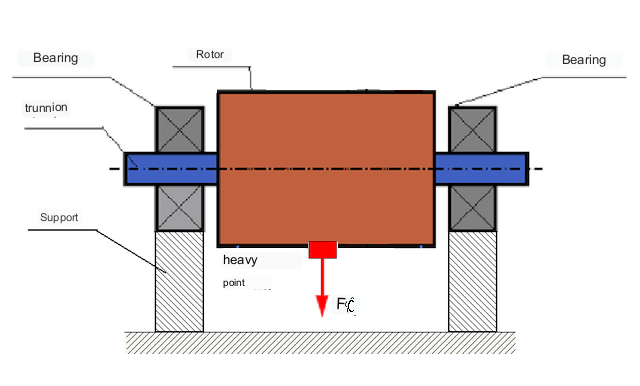
图 2 转子的静态不平衡。
在重力作用下,"重力点 "向下转动
动态不平衡仅在转子旋转时发生。
图 3 显示了转子动态不平衡的例子。
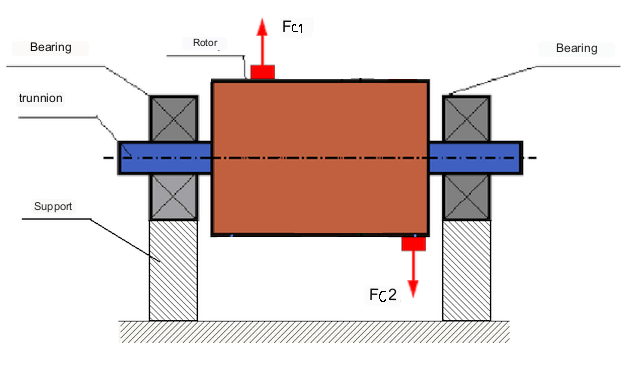
图 3 转子的动态不平衡。
力 Fc1 和 Fc2 产生的力矩会导致转子失衡。
在这种情况下,不平衡的等质量块 M1 和 M2 位于不同的平面上,即位于转子长度方向上的不同位置。在静态位置,即转子不旋转时,只有重力作用在转子上,质量相互平衡。在动力学状态下,当转子旋转时,离心力 Fc1 和 Fc2 开始作用在质量 M1 和 M2 上。这些力大小相等,方向相反。然而,由于它们作用在轴长的不同位置,且不在同一条直线上,因此这些力不能相互补偿。力 Fc1 和 Fc2 会在转子上产生扭矩。因此,这种不平衡也称为力矩不平衡。因此,未补偿的离心力作用在轴承位置上,会大大超出计算值,并缩短轴承的使用寿命。
由于这种不平衡仅在转子旋转过程中动态发生,因此称为动态不平衡。在静态条件下,无法通过 "刀片 "平衡或类似方法来纠正。为了消除动态不平衡,必须安装两个补偿砝码,它们产生的力矩与质量块 M1 和 M2 产生的力矩大小相等、方向相反。补偿砝码的设置不一定要与质量 M1 和 M2 相反且大小相等。最重要的是它们产生的力矩能够完全补偿不平衡力矩。
一般情况下,质量 M1 和 M2 可能互不相等,因此会出现静态和动态不平衡。理论证明,对于刚性转子而言,两个沿转子长度方向间隔开的砝码对于消除其不平衡是必要且足够的。这些砝码既能补偿动态不平衡产生的扭矩,也能补偿质量相对于转子轴线不对称产生的离心力(静态不平衡)。通常,动态不平衡是长转子(如轴)的特点,而静态不平衡则是窄转子的特点。但是,如果窄转子相对于轴线偏斜或变形("八 "字形),则很难消除动态不平衡。(见图 4),因为在这种情况下很难安装能产生必要补偿力矩的校正砝码。
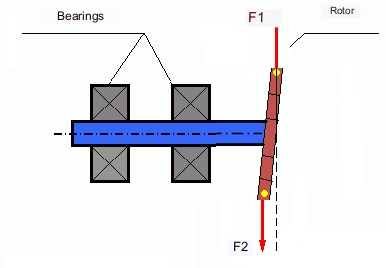
图 4 窄转子的动态不平衡。
力 F1 和 F2 不在同一条直线上,不能相互补偿。
由于转子较窄,产生扭矩的机械臂较小,因此可能需要较大的校正砝码。然而,这也会导致 "诱发不平衡",因为校正砝码的离心力会使窄转子变形。(参见 "刚性转子平衡方法说明(ISO 22061-76)"。第 10 节.转子支撑系统)。)
这一点在风机的窄叶轮上很明显,在这种情况下,除了力不平衡外,空气动力不平衡也会产生。应该理解的是,空气动力不平衡,或者说空气动力与转子的角速度成正比,为了对其进行补偿,需要使用校正质量的离心力,它与角速度的平方成正比。因此,平衡效应只能在特定的平衡频率下产生。在其他旋转频率下会产生额外的误差。
同样,电机中的电磁力也与角速度成正比。因此,不可能通过平衡消除机器振动的所有原因。
机构振动。
振动是机构设计对周期性激振力影响的反应。这种力可以是不同性质的。
不平衡转子产生的离心力是作用在 "重点 "上的一种未补偿的力。通过平衡转子可以消除这种力及其引起的振动。
由于配合部件的制造和装配误差而产生的 "几何 "性质的相互作用力。例如,轴颈的非圆度、齿轮齿形的误差、轴承滚道的波浪度、配合轴的错位等都会产生这些力。在轴颈不圆的情况下,轴的轴线会根据轴的旋转角度发生位移。虽然这种振动在转子转速时也会发生,但几乎不可能通过平衡来消除。
风扇叶轮和其他叶片装置旋转产生的空气动力。液压泵、涡轮机等叶轮旋转产生的水动力。
电机运行时产生的电磁力,如不对称转子绕组、短路绕组等。
振动的幅度(如振幅 Av)不仅取决于以圆周频率 ω 作用在机构上的激振力 Fv,还取决于机构的刚度 k、质量 m 以及阻尼系数 C。
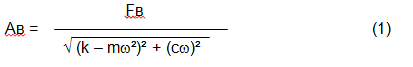
各种类型的传感器可用于测量振动和平衡机制,包括
绝对振动传感器,用于测量振动加速度(加速度计)和振动速度传感器;
相对振动传感器--涡流式或电容式,用于测量振动位移。在某些情况下(当机构设计允许时),力传感器也可用于评估其振动负荷。特别是,它们被广泛用于测量硬轴承平衡机支架的振动负荷。
因此,振动是机器对外力作用的反应。振动的大小不仅取决于作用在机械上的力的大小,还取决于机械设计的刚性。一个相同的力会导致不同的振动。在硬轴承机械中,即使振动很小,轴承也可能承受很大的动态载荷。这就是为什么在平衡硬轴承机床时要使用力传感器而不是振动传感器(振动加速度计)的原因。
振动传感器用于具有相对柔性支撑的机构,此时不平衡离心力的作用会导致支撑的明显变形和振动。力传感器用于刚性支架,此时,即使由于不平衡而产生很大的力,也不会导致明显的振动。
共振是妨碍平衡的一个因素
前面我们提到转子分为刚性和柔性两种。转子的刚度或柔度不应与安装转子的支架(地基)的刚度或移动性相混淆。当转子在离心力作用下的变形(弯曲)可以忽略不计时,转子被认为是刚性的。柔性转子的变形相对较大,无法忽略。
在本文中,我们只考虑刚性转子的平衡问题。刚性(不变形)转子可以安装在刚性或活动(柔性)支架上。显然,支架的刚度/可悬挂性也是相对的,取决于转子的速度和由此产生的离心力的大小。转子支架的自然振动频率是一个有条件的界限。
对于机械系统而言,自然振动的形状和频率由机械系统元件的质量和弹性决定。也就是说,自然振动的频率是机械系统的内部特性,并不取决于外力。在偏离平衡状态时,支撑物会因弹性而趋向于回到平衡位置。但由于巨大转子的惯性,这一过程具有阻尼振动的性质。这些振动是转子-支撑系统的自然振动。其频率取决于转子的质量与支架的弹性之比。
![]()
当转子开始旋转,其旋转频率接近自然振动频率时,振动振幅会急剧增加,从而导致结构破坏。
出现机械共振现象。在共振区域,转速每分钟改变 100 转,振动就会增加数十倍。同时(在共振区域内),振动相位会发生 180° 的变化。
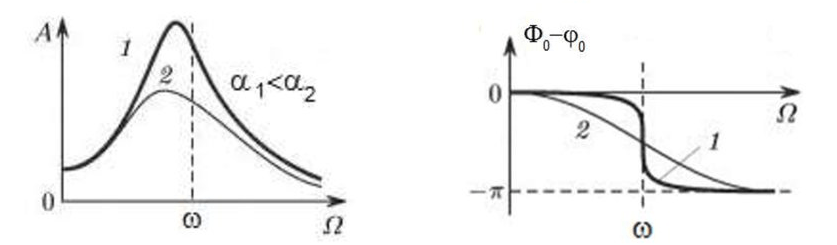
图 5 外力频率变化时机械系统振荡幅度和相位的变化。
如果机械装置的设计不成功,转子的工作频率接近自然振动频率,那么机械装置就会因无法承受的高振动而无法运行。这在通常情况下是不可能的,因为即使是转速的微小变化也会导致振动参数的急剧变化。为了在共振区域进行平衡,需要使用本文未考虑的特殊方法。
可以通过滑行(关闭转子旋转)或冲击法确定机构的自然振动频率,然后对系统的冲击响应进行频谱分析。
对于旋转工作频率高于共振频率的机构,即在共振状态下工作的机构,支架被认为是运动的,测量时使用振动传感器,主要是振动加速度计,测量结构元件的加速度。对于在前共振模式下工作的机构,支架被认为是刚性的。在这种情况下,使用力传感器。
机械系统的线性和非线性模型。非线性是阻碍平衡的一个因素。
在平衡刚性转子时,平衡计算使用的数学模型称为线性模型。线性模型是指在这种模型中,一个量与另一个量成正比(线性)。例如,如果转子上未补偿的质量增加一倍,那么振动值也将增加一倍。对于刚性转子,可以使用线性模型,因为它们不会变形。
对于柔性转子而言,线性模型已不再适用。对于挠性转子,如果重点的质量在旋转过程中增加,就会产生额外的变形,除了质量外,重点位置的半径也会增加。因此,对于柔性转子而言,振动将增加两倍以上,通常的计算方法将不起作用。
此外,支撑物在大变形时的弹性也会发生变化,例如,当支撑物发生小变形时,一些结构元素会起作用,而发生大变形时,其他结构元素也会参与其中。这就是为什么不能平衡没有固定在地基上,而只是放置在地板上的机械装置的原因。如果振动较大,不平衡力会将机械装置拉离地面,从而显著改变系统的刚度特性。电机支脚必须牢牢固定,螺栓安装必须拧紧,垫圈厚度必须提供足够的安装刚度等。如果轴承破损,则可能出现严重的轴错位和冲击,这也会导致线性度变差,无法进行高质量的平衡。
平衡装置和平衡机
如上所述,平衡是将主惯性中心轴与转子旋转轴对准的过程。
这一过程可以通过两种方法进行。
第一种方法是加工转子耳轴,使穿过耳轴中心的轴线与转子的主惯性中心轴线交叉。这种技术在实践中很少使用,本文将不再详细讨论。
第二种(最常见的)方法是移动、安装或拆除转子上的校正砝码,使转子的惯性轴尽可能靠近其旋转轴。
在平衡过程中移动、添加或移除校正砝码可以通过各种技术操作来完成,包括:钻孔、铣削、堆焊、焊接、拧紧或拧松、激光或电子束灼烧、电解、电磁堆焊等。
平衡过程可以通过两种方式实现:
- 使用平衡机对装配好的转子(在轴承中)进行平衡;
- 在平衡机上对转子进行平衡。转子在自身轴承中的平衡通常使用专门的平衡装置(套件),可以测量平衡转子在其旋转频率下的矢量振动,即测量振动的振幅和相位。目前,上述装置是在微处理器技术的基础上制造的,(除了振动测量和分析外)还能自动计算校正砝码的参数,这些砝码应安装在转子上以补偿其不平衡。
这些设备包括
- 基于计算机或工业控制器的测量和计算单元;
- 两个(或更多)振动传感器;
- 相角传感器
- 用于在现场安装传感器的配件;
- 专用软件,设计用于在一个、两个或多个校正平面上执行全周期转子振动参数测量。
目前最常见的平衡机有两种:
- 软支承机(带软支承);
- 硬轴承机床(带刚性支撑)。
软轴承机器具有相对柔韧的支架,例如以扁平弹簧为基础的支架。这些支架的自然振动频率通常比安装在其上的平衡转子的旋转频率低 2-3 倍。在测量机器前共振支架的振动时,通常会使用振动传感器(加速度传感器、振动速度传感器等)。
预共振平衡机使用相对较硬的支架,其自然振动频率应比被平衡转子的旋转频率高 2-3 倍。力传感器通常用于测量预共振机支架的振动负荷。
预共振平衡机的优势在于可以在相对较低的转子转速(最高 400 - 500 rpm)下进行平衡,从而大大简化了机器及其基础的设计,并提高了平衡的生产率和安全性。
平衡刚性转子
重要!
- 平衡只能消除转子质量相对于其旋转轴分布不对称所造成的振动。其他类型的振动无法通过平衡消除!
- 技术机构的设计应确保在旋转工作频率下没有共振,可靠地固定在地基上,安装在可维修的轴承上,并进行平衡。
- 有缺陷的机器必须在平衡前修复。否则,无法实现高质量的平衡。
平衡不能代替维修!
平衡的主要任务是找到承受平衡离心力的补偿砝码的质量和位置。
如上所述,对于刚性转子而言,安装两个补偿砝码通常是必要且足够的。这将消除转子的静态和动态不平衡。平衡期间测量振动的一般方案如下。
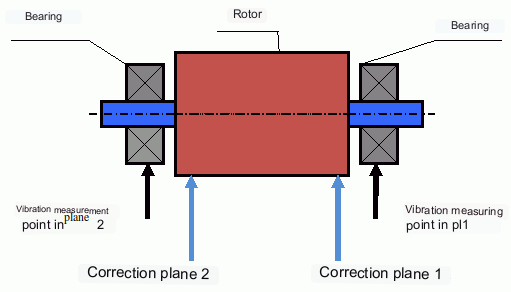
图 6 双平面平衡时测量点和砝码位置(校正平面)的选择
振动传感器安装在 1 号和 2 号点的轴承支架上。转子上通常用反光胶带粘贴一个转速标记。激光转速计利用转速标记来确定转子速度和振动信号的相位。
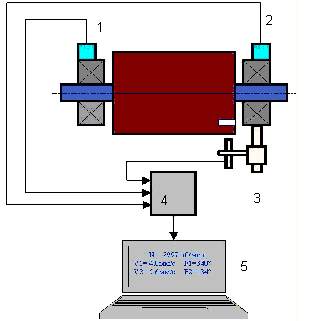
图 7.双平面平衡时传感器的安装。1,2 - 振动传感器,3 - 标记,4 - 测量单元,5 - 笔记本电脑
在大多数情况下,动平衡是通过三次启动法进行的。该方法的基础是在平面 1 和平面 2 上串联放置已知重量的测试砝码,并根据振动参数的变化结果计算砝码的重量和平衡砝码的位置。
安装砝码的位置称为校正平面。校正平面通常选在安装转子的轴承支架区域。
在首次启动时测量初始振动。然后在转子上靠近其中一个轴承的位置放置一个已知重量的测试砝码。进行第二次启动并测量振动参数,这些参数会因安装测试砝码而发生变化。然后移除第一个平面上的测试砝码,将其安装到第二个平面上。进行第三次试运行并测量振动参数。卸下测试砝码后,软件会自动计算平衡砝码的质量和安装角度。
安装测试砝码的目的是确定系统对不平衡变化的反应。测试砝码的重量和位置是已知的,因此软件可以计算出所谓的影响系数,显示引入已知的不平衡如何影响振动参数。影响系数是机械系统本身的特性,取决于支撑的刚度和转子-支撑系统的质量(惯性)。
对于相同设计的同类型机构,影响系数会比较接近。可以将其保存在计算机内存中,用于同类型机构的平衡,而无需进行试运行,从而大大提高了平衡的效率。需要注意的是,在选择试验砝码的质量时,应确保在安装试验砝码时振动参数会发生明显变化。否则,影响系数的计算误差会增大,平衡质量也会下降。
如图 1 所示,离心力沿径向作用,即垂直于转子轴线。因此,必须安装振动传感器,使其敏感轴也指向径向。通常,水平方向的地基刚度较小,因此水平方向的振动较大。因此,为了提高灵敏度,传感器的安装应使其灵敏轴也指向水平方向。虽然没有本质区别。除了径向振动外,还必须监测沿转子旋转轴的轴向振动。这种振动通常不是由不平衡引起的,而是由其他原因引起的,主要与不对中和通过联轴器连接的轴不对中有关。
这种振动无法通过平衡来消除,在这种情况下就需要校准。实际上,这类机器通常同时存在转子不平衡和轴不对中的问题,这使得消除振动的任务变得更加困难。在这种情况下,有必要先将机器对中,然后再进行平衡。(尽管在转矩不平衡较强的情况下,由于基础结构的 "扭曲",轴向也会产生振动)。
我们在其他文章中讨论过用于平衡小型转子的工作台示例:
带软支撑的平衡支架。
平衡电机转子。
转子简易平衡台:设计与应用
评估平衡机制质量的标准。
转子(机构)的平衡质量可以通过两种方法进行评估。第一种方法是将平衡过程中确定的残余不平衡量与残余不平衡公差进行比较。ISO 1940-1-2007 中规定了不同转子等级的公差。第 1 部分。允许不平衡度的定义。
然而,遵守规定的公差并不能完全保证机构的运行可靠性,这与实现最低振动水平有关。这是因为机械装置的振动幅度不仅取决于转子残余不平衡力的大小,还取决于其他几个参数,包括:机械装置结构元件的刚度 k、质量 m、阻尼系数以及旋转频率。因此,在许多情况下,为了估算机械装置的动态质量(包括其平衡质量),建议估算机械装置的残余振动水平。
ISO 10816-3-2002 是规定机械振动允许水平的最常用标准。在该标准的帮助下,可以根据电力驱动的功率为任何类型的机器设定公差。
除这一通用标准外,还有一些针对特定类型机器制定的专门标准。例如,31350-2007、ISO 7919-1-2002 等。
ISO 1940-1-2007。"振动。刚性转子平衡质量要求。第 1 部分。允许不平衡的确定"。
ISO 10816-3:2009 "预览 机械振动 - 通过测量非旋转部件评估机器振动 - 第 3 部分:原位测量时,额定功率大于 15 千瓦且额定转速在 120 r/min 至 15 000 r/min 之间的工业机器"。
ISO 14694:2003《工业风扇--平衡质量和振动等级规范》、
ISO 7919-1-2002 "无往复运动机器的振动。旋转轴的测量和评估标准。通用指南"。






