रोटर संतुलन: स्थैतिक और गतिशील असंतुलन, अनुनाद और व्यावहारिक प्रक्रिया
यह गाइड रोटर बैलेंसिंग के बारे में बताती है। कठोर रोटर"असंतुलन" का क्या अर्थ है, स्थैतिक और गतिशील असंतुलन में क्या अंतर है, अनुनाद और गैर-रैखिकता गुणवत्तापूर्ण परिणाम को कैसे बाधित कर सकते हैं, और संतुलन आमतौर पर एक या दो सुधार तलों में कैसे किया जाता है।.
अंतर्वस्तु
- रोटर क्या होता है और बैलेंसिंग किस चीज को ठीक करती है?
- रोटरों के प्रकार और असंतुलन के प्रकार
- यंत्रों का कंपन: संतुलन से क्या दूर हो सकता है और क्या नहीं।
- अनुनाद: एक ऐसा कारक जो संतुलन को बाधित करता है
- रेखीय बनाम अरैखिक मॉडल: गणनाएँ कब काम करना बंद कर देती हैं
- Balancing devices and balancing machines
- कठोर रोटरों को संतुलित करना (व्यावहारिक नोट्स)
- डायनामिक बैलेंसिंग कैसे की जाती है (तीन-रन विधि)
- संतुलन गुणवत्ता के आकलन के लिए मानदंड
- मानक और संदर्भ
- FAQ
रोटर क्या होता है और बैलेंसिंग किस चीज को ठीक करती है?
The rotor is a body which rotates about some axis and is held by its bearing surfaces in the supports. The bearing surfaces of the rotor transmit loads to the supports via rolling or sliding bearings. The bearing surfaces are the surfaces of the trunnions or the surfaces that replace them.
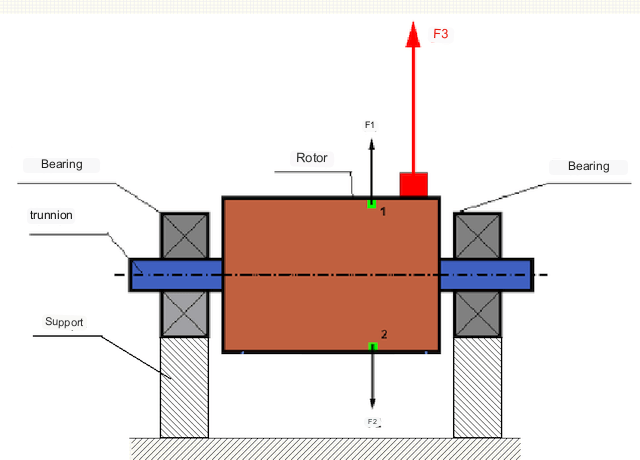
एक पूर्णतः संतुलित रोटर में, उसका द्रव्यमान घूर्णन अक्ष के चारों ओर सममित रूप से वितरित होता है, अर्थात् रोटर के किसी भी तत्व को घूर्णन अक्ष के चारों ओर सममित रूप से स्थित किसी अन्य तत्व से मिलाया जा सकता है। एक संतुलित रोटर में, किसी भी रोटर तत्व पर लगने वाला अपकेंद्रीय बल, सममित तत्व पर लगने वाले अपकेंद्रीय बल द्वारा संतुलित होता है। उदाहरण के लिए, तत्व 1 और 2 (चित्र 1 में हरे रंग से चिह्नित) पर परिमाण में बराबर और दिशा में विपरीत अपकेंद्रीय बल F1 और F2 कार्य करते हैं। यह सभी सममित रोटर तत्वों के लिए सत्य है, और इस प्रकार रोटर पर लगने वाला कुल अपकेंद्रीय बल शून्य होता है और रोटर संतुलित होता है।.
लेकिन यदि रोटर की समरूपता भंग हो जाती है (चित्र 1 में असममित तत्व को लाल रंग से दर्शाया गया है), तो रोटर पर असंतुलित अपकेंद्री बल F3 कार्य करता है। घूर्णन के दौरान, यह बल रोटर के घूर्णन के साथ दिशा बदलता है। इस बल के कारण उत्पन्न गतिशील भार बियरिंग पर स्थानांतरित हो जाता है, जिसके परिणामस्वरूप घिसाव और टूट-फूट में तेजी आती है।.
In addition, under the influence of this variable in direction force there is a cyclic deformation of supports and foundation, on which the rotor is fixed, i.e. there is vibration. In order to eliminate rotor imbalance and the accompanying vibration, balancing masses must be installed to restore symmetry to the rotor.
Rotor balancing is an operation to correct imbalance by adding balancing masses.
The task of balancing is to find the size and location (angle) of one or more balancing masses.
रोटरों के प्रकार और असंतुलन के प्रकार
रोटर सामग्री की मजबूती और उस पर लगने वाले अपकेंद्रीय बलों के परिमाण को ध्यान में रखते हुए, रोटरों को दो प्रकारों में विभाजित किया जा सकता है - कठोर रोटर और लचीले रोटर।.
Rigid rotors deform insignificantly under action of centrifugal force at working modes and influence of this deformation in calculations can be neglected.
लचीले रोटरों के विरूपण को अब नजरअंदाज नहीं किया जा सकता। लचीले रोटरों का विरूपण संतुलन समस्या के समाधान को जटिल बना देता है और कठोर रोटरों के संतुलन की समस्या की तुलना में अन्य गणितीय मॉडलों के अनुप्रयोग की आवश्यकता होती है। यह ध्यान रखना महत्वपूर्ण है कि एक ही रोटर कम गति पर कठोर और उच्च गति पर लचीले रोटर की तरह व्यवहार कर सकता है। आगे हम केवल कठोर रोटरों के संतुलन पर विचार करेंगे।.
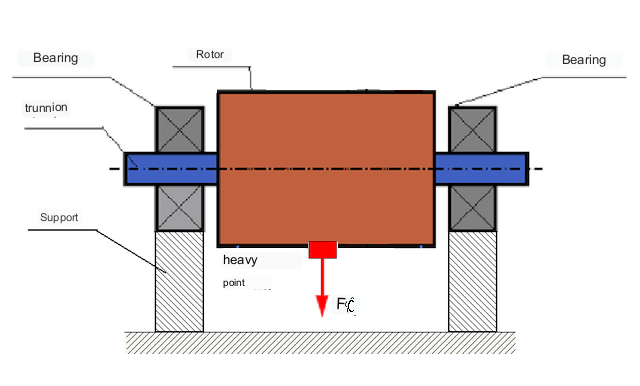
रोटर की लंबाई के अनुदिश असंतुलित द्रव्यमानों के वितरण के आधार पर, दो प्रकार के असंतुलन को पहचाना जा सकता है - स्थैतिक और गतिशील (क्षणिक)। तदनुसार, स्थैतिक और गतिशील रोटर संतुलन का उल्लेख किया जाता है। स्थैतिक रोटर असंतुलन रोटर के घूर्णन के बिना होता है, यानी स्थैतिक अवस्था में, जब गुरुत्वाकर्षण के कारण रोटर का "भारी बिंदु" नीचे की ओर होता है। स्थैतिक असंतुलन वाले रोटर का एक उदाहरण चित्र 2 में दिखाया गया है।
Dynamic unbalance occurs only when the rotor is rotating.
An example of a rotor with dynamic unbalance is shown in Fig. 3.
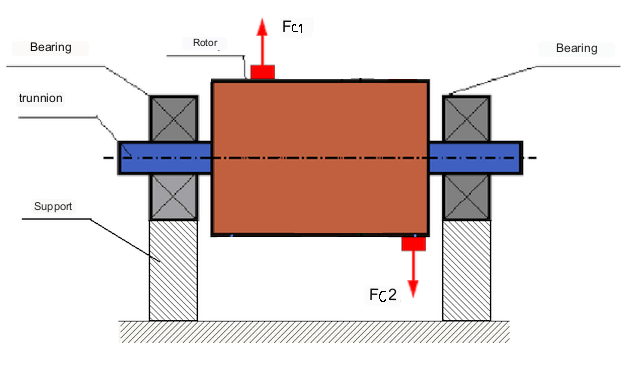
इस स्थिति में, असंतुलित समान द्रव्यमान M1 और M2 रोटर की लंबाई के अनुदिश अलग-अलग तलों में स्थित हैं। स्थिर अवस्था में, यानी जब रोटर घूमता नहीं है, तब केवल गुरुत्वाकर्षण बल ही रोटर पर कार्य करता है और द्रव्यमान एक दूसरे को संतुलित करते हैं। गतिकी में, जब रोटर घूमता है, तब द्रव्यमान M1 और M2 पर अपकेंद्रीय बल Fc1 और Fc2 कार्य करने लगते हैं। ये बल परिमाण में बराबर और दिशा में विपरीत होते हैं। हालांकि, चूंकि ये शाफ्ट की लंबाई के अनुदिश अलग-अलग स्थानों पर लगते हैं और एक ही रेखा में नहीं होते, इसलिए ये बल एक दूसरे को संतुलित नहीं करते। बल Fc1 और Fc2 रोटर पर एक टॉर्क उत्पन्न करते हैं। इसलिए, इस असंतुलन को आघूर्ण असंतुलन भी कहा जाता है। परिणामस्वरूप, बेयरिंग स्थानों पर असंतुलित अपकेंद्रीय बल कार्य करते हैं, जो परिकलित मानों से काफी अधिक हो सकते हैं और बेयरिंग के सेवा जीवन को कम कर सकते हैं।.
क्योंकि इस प्रकार का असंतुलन केवल रोटर के घूर्णन के दौरान गतिशील रूप से होता है, इसलिए इसे गतिशील असंतुलन कहा जाता है। इसे स्थिर अवस्था में "चाकू पर संतुलन" या इसी तरह की विधियों द्वारा ठीक नहीं किया जा सकता है। गतिशील असंतुलन को दूर करने के लिए, दो क्षतिपूर्ति भार स्थापित किए जाने चाहिए, जो द्रव्यमान M1 और M2 से उत्पन्न होने वाले आघूर्ण के बराबर परिमाण और विपरीत दिशा में आघूर्ण उत्पन्न करते हैं। क्षतिपूर्ति भारों को द्रव्यमान M1 और M2 के विपरीत और बराबर परिमाण में स्थापित करना आवश्यक नहीं है। मुख्य बात यह है कि वे एक ऐसा आघूर्ण उत्पन्न करें जो असंतुलन आघूर्ण की पूरी तरह से क्षतिपूर्ति करे।.
सामान्यतः, द्रव्यमान M1 और M2 एक दूसरे के बराबर नहीं होते, इसलिए स्थैतिक और गतिशील असंतुलन का संयोजन होता है। सैद्धांतिक रूप से यह सिद्ध हो चुका है कि एक कठोर रोटर के लिए, रोटर की लंबाई के अनुदिश समान दूरी पर रखे गए दो भार उसके असंतुलन को दूर करने के लिए आवश्यक और पर्याप्त होते हैं। ये भार गतिशील असंतुलन से उत्पन्न टॉर्क और रोटर अक्ष के सापेक्ष द्रव्यमान की विषमता (स्थैतिक असंतुलन) से उत्पन्न अपकेंद्रीय बल दोनों की क्षतिपूर्ति करते हैं। आमतौर पर, गतिशील असंतुलन लंबे रोटरों, जैसे शाफ्ट, की विशेषता है, और स्थैतिक असंतुलन संकरे रोटरों की विशेषता है। हालांकि, यदि संकरा रोटर अक्ष के सापेक्ष तिरछा हो, या विकृत हो ("आठ के आकार का"), तो गतिशील असंतुलन को दूर करना कठिन होगा (चित्र 4 देखें), क्योंकि इस स्थिति में आवश्यक क्षतिपूर्ति बल उत्पन्न करने वाले भारों को स्थापित करना मुश्किल होता है।.
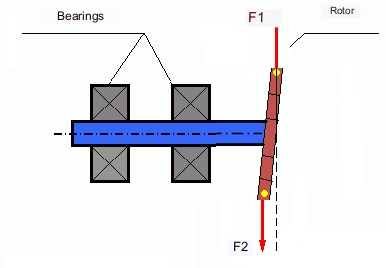
The forces F1 and F2 do not lie on the same line and do not compensate each other.
संकीर्ण रोटर के कारण टॉर्क उत्पन्न करने वाली भुजा छोटी होने की वजह से, बड़े सुधार भार की आवश्यकता हो सकती है। हालाँकि, सुधार भार से उत्पन्न अपकेंद्रीय बलों के कारण संकीर्ण रोटर के विरूपण से "प्रेरित असंतुलन" भी उत्पन्न होता है। (उदाहरण के लिए, "कठोर रोटरों को संतुलित करने के लिए कार्यप्रणाली संबंधी निर्देश (आईएसओ 22061-76 के अनुसार)" अनुभाग 10. रोटर-समर्थन प्रणाली देखें।)
This is noticeable for narrow impellers of fans, in which, in addition to force unbalance, aerodynamic unbalance is also active. And it should be understood that aerodynamic unbalance, or rather aerodynamic force is directly proportional to angular speed of the rotor, and for its compensation the centrifugal force of correcting mass, which is proportional to the square of angular speed, is used. Therefore, the balancing effect can only take place at a specific balancing frequency. At other rotational frequencies there is an additional error.
The same can be said of the electromagnetic forces in an electric motor, which are also proportional to angular velocity. So it is not possible to eliminate all causes of vibration in a machine by balancing.
तंत्रों का कंपन
Vibration is the reaction of the mechanism design to the effects of a cyclic excitatory force. This force can be of different nature.
असंतुलित रोटर के कारण उत्पन्न अपकेंद्रीय बल "भारी बिंदु" पर लगने वाला एक असंतुलित बल है। रोटर को संतुलित करके इस बल और इसके कारण होने वाले कंपन को समाप्त किया जा सकता है।.
पुर्जों के निर्माण और संयोजन में होने वाली त्रुटियों के कारण "ज्यामितीय" प्रकृति के अंतःक्रियात्मक बल उत्पन्न होते हैं। उदाहरण के लिए, ये बल शाफ्ट के गर्दन के गैर-गोलाकार होने, गियर के दांतों के प्रोफाइल में त्रुटियों, बेयरिंग रेसवे की लहरदारता, शाफ्ट के गलत संरेखण आदि के परिणामस्वरूप उत्पन्न हो सकते हैं। जर्नल के गैर-वृत्ताकार होने की स्थिति में, शाफ्ट अक्ष शाफ्ट के घूर्णन कोण के आधार पर विस्थापित हो जाएगा। हालांकि यह कंपन रोटर की गति पर भी होता है, लेकिन संतुलन द्वारा इसे समाप्त करना लगभग असंभव है।.
Aerodynamic forces resulting from the rotation of the impellers of fans and other vane mechanisms. Hydrodynamic forces resulting from the rotation of impellers of hydraulic pumps, turbines, etc.
Electromagnetic forces resulting from the operation of electrical machines, e.g. asymmetric rotor windings, short-circuited windings, etc.
The magnitude of the vibration (e.g. its amplitude Av) depends not only on the excitatory force Fv acting on the mechanism with circular frequency ω, but also on the rigidity k of the mechanism, its mass m , as well as the damping coefficient C.
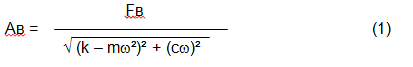
Various types of sensors can be used to measure vibration and balance mechanisms, including:
- absolute vibration sensors designed to measure vibration acceleration (accelerometers) and vibration velocity sensors;
- सापेक्ष कंपन के सेंसर - एड़ी-करंट या कैपेसिटिव, जो कंपन विस्थापन को मापने के लिए डिज़ाइन किए गए हैं;
- कुछ मामलों में (जब तंत्र का डिज़ाइन इसकी अनुमति देता है), बल सेंसर का उपयोग इसके कंपन भार का आकलन करने के लिए भी किया जा सकता है; विशेष रूप से, इनका व्यापक रूप से हार्ड-बेयरिंग बैलेंसिंग मशीन सपोर्ट के कंपन भार को मापने के लिए उपयोग किया जाता है।.
So, vibration is the reaction of a machine to the action of external forces. The magnitude of vibration depends not only on the magnitude of the force acting on the mechanism, but also on the rigidity of the mechanism design. One and the same force can lead to different vibrations. In a hard-bearing machine, even if the vibration is small, the bearings may be subjected to significant dynamic loads. This is why force rather than vibration sensors (vibration accelerometers) are used when balancing hard-bearing machines.
Vibration sensors are used on mechanisms with relatively pliable supports, when the action of unbalanced centrifugal forces leads to a noticeable deformation of supports and vibration. Force sensors are used for rigid supports, when even significant forces due to unbalance do not lead to significant vibration.
Resonance is a factor that prevents balancing
Earlier we mentioned that rotors are divided into rigid and flexible. Stiffness or flexibility of rotor should not be confused with stiffness or mobility of supports (foundation) on which the rotor is installed. A rotor is considered rigid when its deformation (bending) under the action of centrifugal forces can be neglected. Deformation of flexible rotor is relatively large and cannot be neglected.
In this article, we consider only the balancing of rigid rotors. A rigid (non-deformable) rotor can in turn be mounted on rigid or movable (pliable) supports. It is clear that this stiffness/suspendability of supports is also relative, depending on rotor speed and magnitude of resulting centrifugal forces. A conditional boundary is the frequency of natural vibrations of the rotor supports.
For mechanical systems, the shape and frequency of natural vibrations are determined by the mass and the elasticity of the elements of mechanical system. That is, the frequency of natural vibrations is an internal characteristic of the mechanical system and does not depend on external forces. Being deflected from the state of equilibrium, supports due to elasticity tend to return to the position of equilibrium. But due to the inertia of the massive rotor, this process is in the nature of damped oscillations. These vibrations are the natural vibrations of the rotor-support system. Their frequency depends on the ratio of the mass of the rotor to the elasticity of the supports.
When the rotor begins to rotate and the frequency of its rotation approaches the frequency of natural vibrations, the amplitude of vibration increases sharply, which can lead to the destruction of the structure.
The phenomenon of mechanical resonance occurs. In the area of resonance, a change of rotation speed by 100 rpm may lead to an increase in vibration by tens of times. At the same time (in the resonance area) the vibration phase changes by 180°.
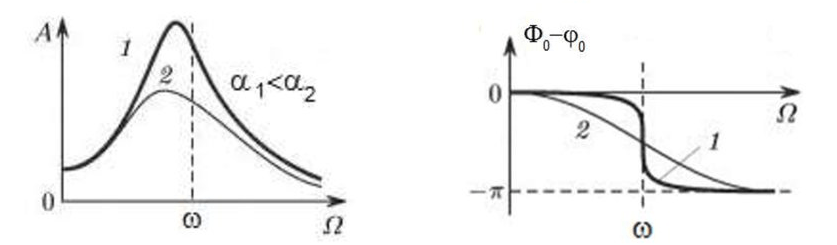
If the design of the mechanism is unsuccessful and the operating frequency of the rotor is close to the frequency of natural vibrations, then the operation of the mechanism becomes impossible because of the inadmissibly high vibration. This is not possible in the usual way, since even a small change in speed will cause a drastic change in the vibration parameters. For balancing in the area of resonance, special methods not considered in this article are used.
It is possible to determine the frequency of natural vibrations of the mechanism at coasting (at switching off the rotor rotation) or by the shock method with the subsequent spectral analysis of the system response to the shock.
For mechanisms, which working frequency of rotation is above the resonance frequency, i.e. working in the resonance regime, the supports are considered to be moving and for measurement are used vibration sensors, mainly vibroacelerometers, measuring acceleration of structural elements. For mechanisms operating in preresonant mode, the supports are considered rigid. In this case, force sensors are used.
Linear and nonlinear models of a mechanical system. Non-linearity is a factor that prevents balancing
When balancing rigid rotors, mathematical models called linear models are used for balancing calculations. A linear model means that in such a model, one quantity is proportional (linear) to the other. For example, if the uncompensated mass on the rotor is doubled, then the vibration value will also be doubled. For rigid rotors, a linear model can be used, since they do not deform.
For flexible rotors, the linear model can no longer be used. For a flexible rotor, if the mass of the heavy point increases during rotation, additional deformation will occur, and in addition to the mass, the radius of the location of the heavy point will also increase. Therefore, for a flexible rotor, the vibration will increase more than twofold, and the usual methods of calculation will not work.
Also, the change of elasticity of supports at their large deformations, for example, when at small deformations of supports some structural elements work, and at large ones other structural elements are involved. This is why you cannot balance mechanisms that are not fixed on a foundation, but, for example, simply placed on the floor. With significant vibrations, the force of the imbalance can pull the mechanism off the floor, thereby significantly changing the stiffness characteristics of the system. Motor feet must be securely fastened, bolt mounts must be tightened, washer thickness must provide sufficient mounting rigidity, etc. If the bearings are broken, significant shaft misalignment and shocks are possible, which will also result in poor linearity and an inability to perform a quality balance.
Balancing devices and balancing machines
जैसा कि ऊपर बताया गया है, संतुलन वह प्रक्रिया है जिसमें जड़त्व की मुख्य केंद्रीय धुरी को रोटर की घूर्णन धुरी के साथ संरेखित किया जाता है।.
This process can be performed by two methods.
The first method involves machining the rotor trunnions in such a way that the axis passing through the centers of the trunnions cross section with the main central axis of inertia of the rotor. Such a technique is rarely used in practice and will not be discussed in detail in this article.
The second (most common) method involves moving, installing or removing correction weights on the rotor, which are placed so that the axis of inertia of the rotor is as close to its axis of rotation as possible.
Moving, adding or removing correction weights during balancing may be accomplished by various technological operations including: drilling, milling, surfacing, welding, screwing or unscrewing, laser or electron beam burning, electrolysis, electromagnetic surfacing, etc.
The balancing process can be accomplished in two ways:
- balancing of assembled rotors (in their own bearings) using balancing machines;
- balancing of rotors on balancing machines. For balancing of rotors in their own bearings usually used specialized balancing devices (kits), which allow to measure the vibration of the balanced rotor at its frequency of rotation in vector form, i.e. to measure both the amplitude and the phase of vibration. At present, the above devices are manufactured on the basis of microprocessor technology and (apart from vibration measurement and analysis) provide automatic calculation of parameters of correcting weights, which should be installed on the rotor to compensate its unbalance.
These devices include:
- a measuring and computing unit based on a computer or industrial controller;
- Two (or more) vibration sensors;
- A phase angle sensor;
- accessories for mounting the sensors on the site;
- specialized software, designed to perform a full cycle of rotor vibration parameters measurement in one, two or more correction planes.
Two types of balancing machines are currently the most common:
- Soft-bearings machines (with soft supports);
- Hard-bearings machines (with rigid supports).
सॉफ्ट-बेयरिंग मशीनों में अपेक्षाकृत लचीले सपोर्ट होते हैं, उदाहरण के लिए, फ्लैट स्प्रिंग पर आधारित सपोर्ट। इन सपोर्टों के प्राकृतिक कंपन की आवृत्ति आमतौर पर उन पर लगे बैलेंसिंग रोटर की घूर्णन आवृत्ति से 2-3 गुना कम होती है। मशीन के प्री-रेजोनेंट सपोर्टों के कंपन को मापने के लिए आमतौर पर कंपन सेंसर (एक्सेलरोमीटर, कंपन वेग सेंसर आदि) का उपयोग किया जाता है।.
Pre-resonance balancing machines use relatively rigid supports, whose natural frequencies of vibration should be 2-3 times higher than the rotation frequency of the rotor being balanced. Force transducers are usually used to measure the vibration load of the preresonance machine supports.
प्री-रेजोनेंस बैलेंसिंग मशीनों का लाभ यह है कि उन पर बैलेंसिंग अपेक्षाकृत कम रोटर गति (400 - 500 आरपीएम तक) पर की जा सकती है, जो मशीन और उसके आधार के डिजाइन को काफी सरल बनाती है, और बैलेंसिंग की उत्पादकता और सुरक्षा को बढ़ाती है।.
Balancing rigid rotors
Important!
- Balancing only eliminates vibration caused by asymmetrical distribution of the rotor mass relative to its rotational axis. Other types of vibration are not eliminated by balancing!
- Technical mechanisms, whose design ensures the absence of resonances at the operating frequency of rotation, reliably fixed on the foundation, installed in serviceable bearings, are subject to balancing.
- Defective machinery must be repaired before balancing. Otherwise, quality balancing is not possible.
Balancing is no substitute for repair!
The main task of balancing is to find the mass and location of compensating weights that are subject to balancing centrifugal forces.
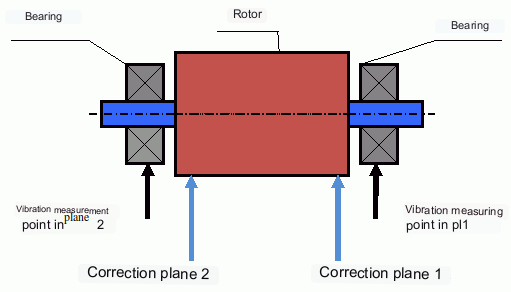
As mentioned above, for rigid rotors, it is generally necessary and sufficient to install two compensating weights. This will eliminate both static and dynamic unbalance of the rotor. The general scheme for measuring vibration during balancing is as follows.
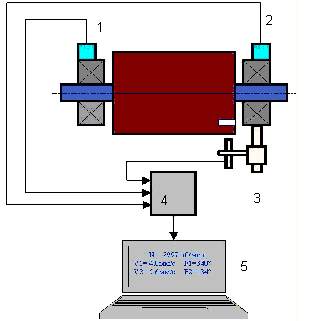
Vibration sensors are installed on the bearing supports at points 1 and 2. A revolution marker is attached to the rotor, usually with reflective tape. The RPM mark is used by the laser tachometer to determine the rotor speed and phase of the vibration signal.
डायनामिक बैलेंसिंग कैसे की जाती है (तीन-रन विधि)
In most cases dynamic balancing is carried out by the method of three starts. The method is based on the fact that test weights of known weight are placed on the rotor in series in plane 1 and 2 and the weights and the location of the balancing weights are calculated based on the results of changes in the vibration parameters.
The place of installation of weights is called the correction plane. Usually the correction planes are selected in the area of the bearing supports on which the rotor is installed.
At the first start-up the initial vibration is measured. Then a test weight of known weight is placed on the rotor closer to one of the bearings. A second start-up is carried out and the vibration parameters are measured, which should change due to the test weight installation. Then the test weight in the first plane is removed and installed in the second plane. A third test run is performed and the vibration parameters are measured. The test weight is removed and the software automatically calculates the masses and installation angles of the balance weights.
The point of installing the test weights is to determine how the system reacts to changes in imbalance. The weights and locations of the test weights are known, so the software can calculate so called influence coefficients, showing how introducing a known imbalance affects the vibration parameters. The influence coefficients are characteristics of the mechanical system itself and depend on the rigidity of the supports and the mass (inertia) of the rotor-support system.
For the same type of mechanisms of the same design the influence coefficients will be close. It is possible to save them in the computer memory and use them for balancing of the same-type mechanisms without test runs, which significantly increases the productivity of balancing. Note that the mass of test weights should be chosen such that the vibration parameters change noticeably when test weights are installed. Otherwise, the error of calculation of influence coefficients increases and the quality of balancing deteriorates.
As you can see from Fig. 1, the centrifugal force acts in the radial direction, i.e. perpendicular to the rotor axis. Therefore, the vibration sensors must be installed so that their axis of sensitivity also points in the radial direction. Usually, the stiffness of the foundation in the horizontal direction is less, so the vibration in the horizontal direction is higher. Therefore, in order to increase the sensitivity, the sensors should be installed so that their axis of sensitivity is also directed horizontally. Although there is no fundamental difference. In addition to vibration in the radial direction, vibration in the axial direction, along the rotor rotation axis, must be monitored. This vibration is usually not caused by unbalance, but by other causes, mainly related to misalignment and misalignment of the shafts connected through the coupling.
संतुलन द्वारा इस कंपन को समाप्त नहीं किया जा सकता, इसलिए संरेखण आवश्यक है। व्यवहार में, ऐसी मशीनों में आमतौर पर रोटर असंतुलन और शाफ्ट मिसअलाइनमेंट दोनों होते हैं, जिससे कंपन को समाप्त करना और भी कठिन हो जाता है। ऐसे मामलों में, पहले मशीन को केंद्र में लाना और फिर उसे संतुलित करना आवश्यक है। (हालांकि, तीव्र टॉर्क असंतुलन होने पर, आधार संरचना के "घुमाव" के कारण अक्षीय दिशा में भी कंपन होता है।)
संबंधित लेख (संतुलन स्टैंड के उदाहरण)
- मुलायम सहारे वाला संतुलन स्टैंड
- विद्युत मोटरों के रोटरों को संतुलित करना
- Simple but effective balancing stands
संतुलन तंत्र की गुणवत्ता का आकलन करने के लिए मानदंड
The balancing quality of rotors (mechanisms) can be evaluated in two ways. The first method involves comparing the amount of residual unbalance determined during the balancing process with the tolerance for residual unbalance. These tolerances for the different rotor classes are specified in ISO 1940-1-2007. Part 1. Definition of allowable unbalance.
However, compliance with the specified tolerances cannot fully guarantee the operational reliability of the mechanism, associated with the achievement of the minimum level of its vibration. This is explained by the fact that the magnitude of vibration of the mechanism is determined not only by the magnitude of the force associated with the residual unbalance of its rotor, but also depends on several other parameters, including: the rigidity k of the mechanism structural elements, its mass m, the damping factor, as well as the rotation frequency. Therefore, to estimate dynamic qualities of the mechanism (including quality of its balance) in a number of cases it is recommended to estimate the level of residual vibration of the mechanism, which is regulated by a number of standards.
The most common standard, which regulates the admissible levels of vibration of mechanisms is ISO 10816-3-2002. With its help, it is possible to set tolerances for any type of machines, taking into account the power of their electric drive.
In addition to this universal standard, there is a number of specialized standards developed for specific types of machines. For example, 31350-2007 , ISO 7919-1-2002, etc.
मानक और संदर्भ
- आईएसओ 1940-1:2007. कंपन। कठोर रोटरों की संतुलन गुणवत्ता के लिए आवश्यकताएँ। भाग 1. अनुमेय असंतुलन का निर्धारण।.
- आईएसओ 10816-3:2009. यांत्रिक कंपन — गैर-घूर्णन भागों पर माप द्वारा मशीन कंपन का मूल्यांकन — भाग 3: 15 किलोवाट से अधिक नाममात्र शक्ति और 120 आर/मिनट और 15 000 आर/मिनट के बीच नाममात्र गति वाली औद्योगिक मशीनें, जब मौके पर ही मापी जाती हैं।.
- आईएसओ 14694:2003. औद्योगिक पंखे — संतुलन गुणवत्ता और कंपन स्तरों के लिए विशिष्टताएँ।.
- आईएसओ 7919-1:2002. प्रत्यावर्ती गति के बिना मशीनों का कंपन — घूर्णनशील शाफ्टों पर माप और मूल्यांकन मानदंड — सामान्य मार्गदर्शन।.
FAQ
क्या बैलेंसिंग से कंपन पूरी तरह खत्म हो जाता है?
नहीं। बैलेंसिंग प्रक्रिया रोटर के द्रव्यमान के उसके घूर्णन अक्ष के सापेक्ष असममित वितरण के कारण होने वाले कंपन को दूर करती है। गलत संरेखण, बेयरिंग दोष, वायुगतिकीय/जलगतिकीय बल, विद्युत चुम्बकीय बल और अन्य कारणों से उत्पन्न कंपन के लिए अलग निदान और सुधारात्मक कार्रवाई की आवश्यकता होती है।.
अनुनाद के निकट संतुलन विफल क्यों हो सकता है?
अनुनाद के निकट, गति में मामूली बदलाव से कंपन आयाम में बड़े परिवर्तन और 180 डिग्री का कला विस्थापन हो सकता है। ऐसी स्थितियों में मापन परिणाम अस्थिर हो जाते हैं, और विशेष विधियों के बिना पारंपरिक संतुलन प्रक्रियाएं अभिसरित नहीं हो सकती हैं।.
आपको एक-प्लेन बनाम दो-प्लेन संतुलन की आवश्यकता कब होती है?
एक कठोर रोटर के लिए, रोटर की लंबाई के अनुदिश अलग-अलग रखे गए दो भार आमतौर पर संयुक्त स्थैतिक और गतिशील असंतुलन को दूर करने के लिए आवश्यक और पर्याप्त होते हैं। संकरे रोटर अक्सर मुख्य रूप से स्थैतिक असंतुलन प्रदर्शित करते हैं, लेकिन विरूपण और ज्यामिति एक गतिशील घटक को जन्म दे सकते हैं जिसके लिए दो-तलीय सुधार की आवश्यकता हो सकती है।.
संतुलन करने से पहले क्या करना चाहिए?
सुनिश्चित करें कि मशीन चालू हालत में है: नींव पर मज़बूती से लगी हुई हो, बेयरिंग सही हों, कोई गंभीर ढीलापन न हो, और अनियमितता का कोई स्पष्ट कारण न हो। बैलेंसिंग मरम्मत का विकल्प नहीं है।.
चाबी छीनना
- संतुलन द्रव्यमान-संबंधी (अपकेंद्री) उत्तेजना को ठीक करता है; यह गलत संरेखण, बेयरिंग क्षति, या विद्युत चुम्बकीय/वायुगतिकीय स्रोतों की समस्या का समाधान नहीं करता है।.
- अनुनाद और गैर-रैखिकता पारंपरिक संतुलन को अप्रभावी या असुरक्षित बना सकते हैं।.
- कठोर रोटरों के लिए, दो-तल संतुलन संयुक्त स्थैतिक + गतिशील असंतुलन का सामान्य समाधान है।.






