Equilibratura del rotore: squilibrio statico e dinamico, risonanza e procedura pratica
Questa guida spiega il bilanciamento del rotore per rotori rigidi: cosa significa “sbilanciamento”, come differiscono lo sbilanciamento statico e quello dinamico, perché la risonanza e la non linearità possono impedire un risultato di qualità e come il bilanciamento viene in genere eseguito su uno o due piani di correzione.
Contenuto
- Cos'è un rotore e cosa corregge l'equilibratura?
- Tipi di rotori e tipi di squilibrio
- Vibrazione dei meccanismi: cosa può e cosa non può rimuovere il bilanciamento
- Risonanza: un fattore che impedisce l'equilibrio
- Modelli lineari vs. non lineari: quando i calcoli smettono di funzionare
- Dispositivi di bilanciamento e macchine di bilanciamento
- Bilanciamento dei rotori rigidi (note pratiche)
- Come viene eseguito il bilanciamento dinamico (metodo a tre passaggi)
- Criteri per la valutazione della qualità del bilanciamento
- Standard e riferimenti
- FAQ
Cos'è un rotore e cosa corregge l'equilibratura?
Il rotore è un corpo che ruota attorno a un asse ed è sostenuto dalle sue superfici portanti nei supporti. Le superfici portanti del rotore trasmettono i carichi ai supporti mediante cuscinetti volventi o scorrevoli. Le superfici portanti sono le superfici dei perni o le superfici che li sostituiscono.
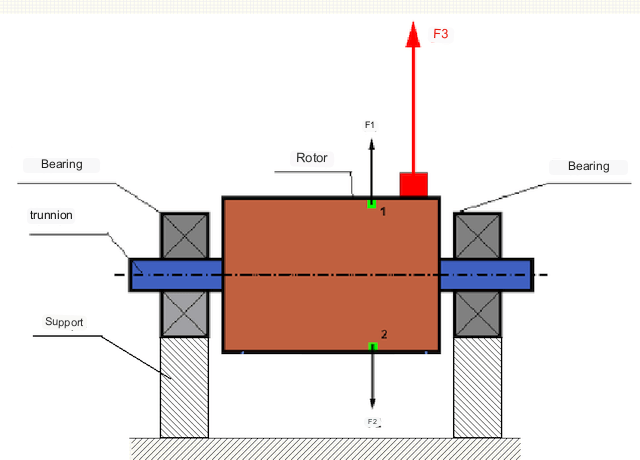
In un rotore perfettamente bilanciato, la sua massa è distribuita simmetricamente rispetto all'asse di rotazione, ovvero qualsiasi elemento del rotore può essere abbinato a un altro elemento posizionato simmetricamente rispetto all'asse di rotazione. In un rotore bilanciato, la forza centrifuga agente su qualsiasi elemento del rotore è bilanciata dalla forza centrifuga agente sull'elemento simmetrico. Ad esempio, le forze centrifughe F1 e F2, di uguale intensità e direzione opposta, agiscono sugli elementi 1 e 2 (contrassegnati in verde in Fig. 1). Questo vale per tutti gli elementi simmetrici del rotore, e quindi la forza centrifuga totale agente sul rotore è 0 e il rotore è bilanciato.
Tuttavia, se la simmetria del rotore è interrotta (l'elemento asimmetrico è contrassegnato in rosso nella Figura 1), sul rotore agisce una forza centrifuga sbilanciata F3. Durante la rotazione, questa forza cambia direzione con la rotazione del rotore. Il carico dinamico risultante da questa forza viene trasmesso ai cuscinetti, con conseguente usura accelerata.
Inoltre, sotto l'influenza di questa forza di direzione variabile, si verifica una deformazione ciclica dei supporti e delle fondamenta, su cui è fissato il rotore, ovvero si verificano vibrazioni. Per eliminare lo squilibrio del rotore e le vibrazioni che lo accompagnano, è necessario installare masse di bilanciamento per ripristinare la simmetria del rotore.
L'equilibratura del rotore è un'operazione di correzione dello squilibrio mediante l'aggiunta di masse di bilanciamento.
Il compito del bilanciamento consiste nel trovare la dimensione e la posizione (angolo) di una o più masse di bilanciamento.
Tipi di rotori e tipi di squilibrio
Tenendo conto della resistenza del materiale del rotore e dell'entità delle forze centrifughe che agiscono su di esso, i rotori possono essere suddivisi in due tipi: rigidi e flessibili.
I rotori rigidi si deformano in modo insignificante sotto l'azione della forza centrifuga nei modi di lavoro e l'influenza di questa deformazione nei calcoli può essere trascurata.
La deformazione dei rotori flessibili non può più essere trascurata. La deformazione dei rotori flessibili complica la soluzione del problema di bilanciamento e richiede l'applicazione di modelli matematici diversi rispetto al problema di bilanciamento dei rotori rigidi. È importante notare che lo stesso rotore a basse velocità può comportarsi come rigido e ad alte velocità come flessibile. Di seguito, considereremo solo il bilanciamento dei rotori rigidi.
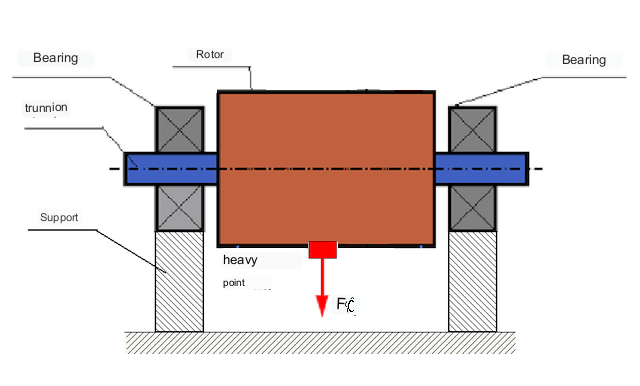
A seconda della distribuzione delle masse sbilanciate lungo la lunghezza del rotore, si possono distinguere due tipi di sbilanciamento: statico e dinamico (momentaneo). Di conseguenza, si parla di sbilanciamento statico e dinamico del rotore. Lo sbilanciamento statico del rotore si verifica senza rotazione del rotore, ovvero, in statica, quando il rotore viene invertito dalla gravità con il suo "punto pesante" rivolto verso il basso. Un esempio di rotore con sbilanciamento statico è mostrato in Fig. 2.
Lo squilibrio dinamico si verifica solo quando il rotore è in rotazione.
Un esempio di rotore con squilibrio dinamico è illustrato nella Fig. 3.
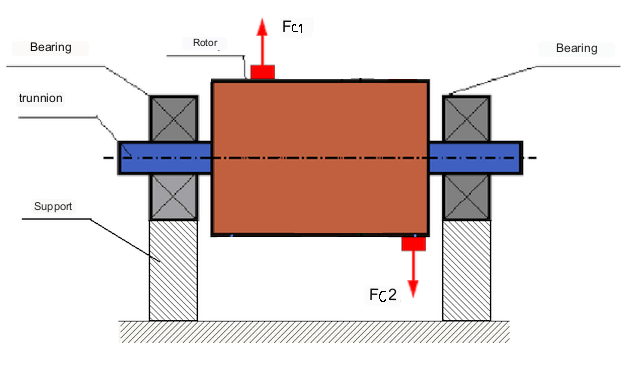
In questo caso, le masse uguali sbilanciate M1 e M2 si trovano su piani diversi, in punti diversi lungo la lunghezza del rotore. In posizione statica, ovvero quando il rotore non ruota, solo la gravità agisce sul rotore e le masse si bilanciano a vicenda. In dinamica, quando il rotore ruota, le forze centrifughe Fc1 e Fc2 iniziano ad agire sulle masse M1 e M2. Queste forze sono di uguale intensità e di direzione opposta. Tuttavia, poiché sono applicate in punti diversi lungo la lunghezza dell'albero e non sono sulla stessa linea, queste forze non si compensano a vicenda. Le forze Fc1 e Fc2 creano una coppia applicata al rotore. Pertanto, questo squilibrio è anche chiamato squilibrio di momento. Di conseguenza, forze centrifughe non compensate agiscono sulle posizioni dei cuscinetti, che possono superare notevolmente i valori calcolati e ridurre la durata dei cuscinetti.
Poiché questo tipo di squilibrio si verifica solo dinamicamente durante la rotazione del rotore, è chiamato squilibrio dinamico. Non può essere corretto in condizioni statiche mediante equilibratura "a coltelli" o metodi simili. Per eliminare lo squilibrio dinamico, è necessario installare due masse di compensazione, che producono un momento di intensità uguale e verso opposto al momento generato dalle masse M1 e M2. Le masse di compensazione non devono essere necessariamente disposte in intensità opposta e uguale alle masse M1 e M2. L'importante è che producano un momento che compensi completamente il momento di squilibrio.
In generale, le masse M1 e M2 potrebbero non essere uguali tra loro, quindi si verificherà una combinazione di squilibrio statico e dinamico. È teoricamente dimostrato che per un rotore rigido, due pesi distanziati lungo la lunghezza del rotore sono necessari e sufficienti per eliminarne lo squilibrio. Questi pesi compenseranno sia la coppia risultante dallo squilibrio dinamico sia la forza centrifuga risultante dall'asimmetria della massa rispetto all'asse del rotore (squilibrio statico). Tipicamente, lo squilibrio dinamico è caratteristico dei rotori lunghi, come gli alberi, mentre lo squilibrio statico è caratteristico dei rotori stretti. Tuttavia, se il rotore stretto è inclinato rispetto all'asse o deformato ("a forma di otto"), lo squilibrio dinamico sarà difficile da eliminare (vedi Fig. 4), perché in questo caso è difficile installare pesi correttori che creino il momento di compensazione necessario.
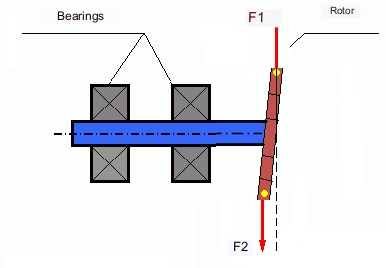
Le forze F1 e F2 non giacciono sulla stessa linea e non si compensano a vicenda.
Poiché il braccio per generare la coppia è piccolo a causa del rotore stretto, potrebbero essere necessari pesi di correzione di grandi dimensioni. Tuttavia, ciò si traduce anche in uno "squilibrio indotto" dovuto alla deformazione del rotore stretto dovuta alle forze centrifughe generate dai pesi di correzione. (Vedi ad esempio "Istruzioni metodologiche per l'equilibratura di rotori rigidi (secondo ISO 22061-76)". Sezione 10. SISTEMA DI SUPPORTO DEL ROTORE.)
Ciò è evidente per le giranti strette dei ventilatori, in cui, oltre allo squilibrio di forza, è attivo anche lo squilibrio aerodinamico. Si deve comprendere che lo squilibrio aerodinamico, o meglio la forza aerodinamica, è direttamente proporzionale alla velocità angolare del rotore, e per la sua compensazione si utilizza la forza centrifuga della massa correttrice, che è proporzionale al quadrato della velocità angolare. Pertanto, l'effetto di bilanciamento può avvenire solo a una specifica frequenza di bilanciamento. Ad altre frequenze di rotazione si verifica un errore aggiuntivo.
Lo stesso vale per le forze elettromagnetiche di un motore elettrico, anch'esse proporzionali alla velocità angolare. Non è quindi possibile eliminare tutte le cause di vibrazione di una macchina mediante l'equilibratura.
Vibrazione dei meccanismi
La vibrazione è la reazione della struttura del meccanismo agli effetti di una forza eccitatoria ciclica. Questa forza può essere di diversa natura.
La forza centrifuga risultante dallo sbilanciamento del rotore è una forza non compensata che agisce sul "punto pesante". È questa forza e le vibrazioni da essa causate che possono essere eliminate bilanciando il rotore.
Forze di interazione di natura "geometrica" derivanti da errori di fabbricazione e assemblaggio delle parti accoppiate. Queste forze possono, ad esempio, derivare dalla non circolarità dei colli degli alberi, da errori nei profili dei denti degli ingranaggi, dall'ondulazione delle piste dei cuscinetti, dal disallineamento degli alberi accoppiati, ecc. In caso di non circolarità dei perni, l'asse dell'albero verrà spostato in base all'angolo di rotazione dell'albero. Sebbene questa vibrazione si verifichi anche alla velocità del rotore, è quasi impossibile eliminarla mediante bilanciamento.
Forze aerodinamiche derivanti dalla rotazione delle giranti dei ventilatori e di altri meccanismi a palette. Forze idrodinamiche derivanti dalla rotazione delle giranti di pompe idrauliche, turbine, ecc.
Forze elettromagnetiche derivanti dal funzionamento delle macchine elettriche, ad esempio avvolgimenti asimmetrici del rotore, avvolgimenti in cortocircuito, ecc.
L'entità della vibrazione (ad esempio la sua ampiezza Av) dipende non solo dalla forza eccitatoria Fv che agisce sul meccanismo con frequenza circolare ω, ma anche dalla rigidità k del meccanismo, dalla sua massa m , nonché dal coefficiente di smorzamento C.
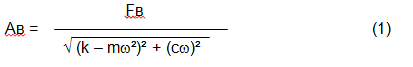
Per misurare le vibrazioni e i meccanismi di equilibrio si possono utilizzare diversi tipi di sensori, tra cui:
- sensori di vibrazione assoluti progettati per misurare l'accelerazione delle vibrazioni (accelerometri) e sensori di velocità delle vibrazioni;
- sensori di vibrazione relativa - a correnti parassite o capacitivi, progettati per misurare lo spostamento delle vibrazioni;
- in alcuni casi (quando la progettazione del meccanismo lo consente), i sensori di forza possono essere utilizzati anche per valutare il carico di vibrazione; in particolare, sono ampiamente utilizzati per misurare il carico di vibrazione dei supporti rigidi delle macchine di bilanciamento.
La vibrazione è quindi la reazione di una macchina all'azione di forze esterne. L'entità della vibrazione dipende non solo dall'entità della forza che agisce sul meccanismo, ma anche dalla rigidità della struttura del meccanismo. Una stessa forza può provocare vibrazioni diverse. In una macchina con cuscinetti rigidi, anche se la vibrazione è piccola, i cuscinetti possono essere sottoposti a carichi dinamici significativi. Per questo motivo, nel bilanciamento delle macchine a cuscinetti rigidi si utilizzano sensori di forza piuttosto che di vibrazione (accelerometri a vibrazione).
I sensori di vibrazione sono utilizzati su meccanismi con supporti relativamente malleabili, quando l'azione di forze centrifughe sbilanciate porta a una notevole deformazione dei supporti e a vibrazioni. I sensori di forza sono utilizzati per supporti rigidi, quando anche forze significative dovute allo squilibrio non portano a vibrazioni significative.
La risonanza è un fattore che impedisce il bilanciamento
In precedenza abbiamo detto che i rotori si dividono in rigidi e flessibili. La rigidità o la flessibilità del rotore non deve essere confusa con la rigidità o la mobilità dei supporti (fondamenta) su cui il rotore è installato. Un rotore è considerato rigido quando la sua deformazione (flessione) sotto l'azione delle forze centrifughe può essere trascurata. La deformazione di un rotore flessibile è relativamente grande e non può essere trascurata.
In questo articolo consideriamo solo il bilanciamento di rotori rigidi. Un rotore rigido (indeformabile) può a sua volta essere montato su supporti rigidi o mobili (malleabili). È chiaro che anche la rigidità/sospensione dei supporti è relativa, in funzione della velocità del rotore e dell'entità delle forze centrifughe risultanti. Un limite condizionato è la frequenza delle vibrazioni naturali dei supporti del rotore.
Per i sistemi meccanici, la forma e la frequenza delle vibrazioni naturali sono determinate dalla massa e dall'elasticità degli elementi del sistema meccanico. In altre parole, la frequenza delle vibrazioni naturali è una caratteristica interna del sistema meccanico e non dipende da forze esterne. Se deviati dallo stato di equilibrio, i supporti, grazie all'elasticità, tendono a tornare alla posizione di equilibrio. Ma a causa dell'inerzia del rotore massiccio, questo processo ha la natura di oscillazioni smorzate. Queste vibrazioni sono le vibrazioni naturali del sistema rotore-supporto. La loro frequenza dipende dal rapporto tra la massa del rotore e l'elasticità dei supporti.
Quando il rotore inizia a ruotare e la frequenza di rotazione si avvicina alla frequenza delle vibrazioni naturali, l'ampiezza delle vibrazioni aumenta bruscamente e può portare alla distruzione della struttura.
Si verifica il fenomeno della risonanza meccanica. Nell'area di risonanza, una variazione della velocità di rotazione di 100 giri/min può portare a un aumento delle vibrazioni di decine di volte. Allo stesso tempo (nell'area di risonanza) la fase di vibrazione cambia di 180°.
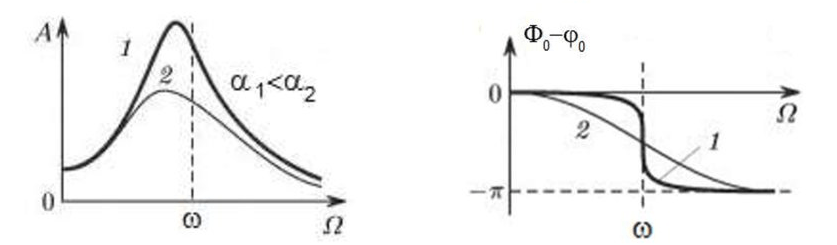
Se la progettazione del meccanismo non è riuscita e la frequenza operativa del rotore è vicina alla frequenza delle vibrazioni naturali, il funzionamento del meccanismo diventa impossibile a causa delle vibrazioni troppo elevate. Questo non è possibile nel modo consueto, poiché anche una piccola variazione di velocità provoca un drastico cambiamento dei parametri di vibrazione. Per il bilanciamento nell'area di risonanza, si utilizzano metodi speciali non considerati in questo articolo.
È possibile determinare la frequenza delle vibrazioni naturali del meccanismo in fase di arresto (per l'interruzione della rotazione del rotore) o con il metodo dell'urto, con la successiva analisi spettrale della risposta del sistema all'urto.
Per i meccanismi la cui frequenza di rotazione è superiore alla frequenza di risonanza, cioè che lavorano in regime di risonanza, i supporti sono considerati in movimento e per la misurazione si utilizzano sensori di vibrazione, principalmente vibroacelerometri, che misurano l'accelerazione degli elementi strutturali. Per i meccanismi che operano in regime di prerisonanza, i supporti sono considerati rigidi. In questo caso si utilizzano sensori di forza.
Modelli lineari e non lineari di un sistema meccanico. La non linearità è un fattore che impedisce il bilanciamento
Per il bilanciamento dei rotori rigidi, per i calcoli di bilanciamento si utilizzano modelli matematici chiamati modelli lineari. Un modello lineare significa che una grandezza è proporzionale (lineare) all'altra. Ad esempio, se la massa non compensata del rotore viene raddoppiata, anche il valore delle vibrazioni sarà raddoppiato. Per i rotori rigidi è possibile utilizzare un modello lineare, poiché non si deformano.
Per i rotori flessibili, il modello lineare non può più essere utilizzato. Per un rotore flessibile, se la massa del punto pesante aumenta durante la rotazione, si verificherà un'ulteriore deformazione e, oltre alla massa, aumenterà anche il raggio della posizione del punto pesante. Pertanto, nel caso di un rotore flessibile, le vibrazioni aumentano di oltre due volte e i metodi di calcolo abituali non funzionano.
Inoltre, il cambiamento di elasticità dei supporti alle loro grandi deformazioni, ad esempio, quando a piccole deformazioni dei supporti alcuni elementi strutturali lavorano, e a grandi deformazioni altri elementi strutturali sono coinvolti. Per questo motivo non è possibile bilanciare meccanismi che non sono fissati su una fondazione, ma, ad esempio, semplicemente appoggiati sul pavimento. In caso di vibrazioni significative, la forza dello squilibrio può staccare il meccanismo dal pavimento, modificando in modo significativo le caratteristiche di rigidità del sistema. I piedini del motore devono essere fissati saldamente, i supporti dei bulloni devono essere serrati, lo spessore delle rondelle deve garantire una rigidità di montaggio sufficiente, ecc. Se i cuscinetti sono rotti, è possibile che si verifichino notevoli disallineamenti dell'albero e urti, con conseguente scarsa linearità e incapacità di eseguire un bilanciamento di qualità.
Dispositivi di bilanciamento e macchine di bilanciamento
Come accennato in precedenza, il bilanciamento è il processo di allineamento dell'asse centrale principale di inerzia con l'asse di rotazione del rotore.
Questo processo può essere eseguito con due metodi.
Il primo metodo prevede la lavorazione dei troni del rotore in modo tale che l'asse passante per i centri dei troni incroci la sezione con l'asse centrale principale di inerzia del rotore. Questa tecnica è raramente utilizzata nella pratica e non sarà discussa in dettaglio in questo articolo.
Il secondo metodo (il più comune) prevede lo spostamento, l'installazione o la rimozione di pesi correttivi sul rotore, che vengono posizionati in modo che l'asse di inerzia del rotore sia il più vicino possibile al suo asse di rotazione.
Lo spostamento, l'aggiunta o la rimozione dei pesi di correzione durante l'equilibratura può essere realizzato mediante varie operazioni tecnologiche, tra cui: foratura, fresatura, rivestimento, saldatura, avvitamento o svitamento, bruciatura con laser o fascio di elettroni, elettrolisi, rivestimento elettromagnetico, ecc.
Il processo di bilanciamento può essere realizzato in due modi:
- equilibratura di rotori assemblati (nei propri cuscinetti) mediante macchine equilibratrici;
- bilanciamento dei rotori su macchine equilibratrici. Per il bilanciamento dei rotori nei propri cuscinetti si utilizzano solitamente dispositivi di bilanciamento specializzati (kit), che consentono di misurare la vibrazione del rotore bilanciato alla sua frequenza di rotazione in forma vettoriale, ossia di misurare sia l'ampiezza che la fase della vibrazione. Attualmente, i dispositivi di cui sopra sono prodotti sulla base della tecnologia dei microprocessori e (oltre alla misurazione e all'analisi delle vibrazioni) forniscono il calcolo automatico dei parametri dei pesi correttivi che devono essere installati sul rotore per compensarne lo squilibrio.
Questi dispositivi includono:
- un'unità di misura e di calcolo basata su un computer o un controllore industriale;
- Due (o più) sensori di vibrazione;
- Un sensore di angolo di fase;
- accessori per il montaggio dei sensori sul sito;
- software specializzato, progettato per eseguire un ciclo completo di misurazione dei parametri di vibrazione del rotore in uno, due o più piani di correzione.
Attualmente, le macchine di bilanciamento più diffuse sono di due tipi:
- Macchine a cuscinetti morbidi (con supporti morbidi);
- Macchine a cuscinetti rigidi (con supporti rigidi).
Le macchine con cuscinetti morbidi hanno supporti relativamente flessibili, ad esempio basati su molle piatte. La frequenza delle vibrazioni naturali di questi supporti è solitamente 2-3 volte inferiore alla frequenza di rotazione del rotore di bilanciamento, che è montato su di essi. Per misurare le vibrazioni dei supporti pre-risonanti della macchina, vengono solitamente utilizzati sensori di vibrazione (accelerometri, sensori di velocità di vibrazione, ecc.).
Le macchine di equilibratura a prerisonanza utilizzano supporti relativamente rigidi, le cui frequenze naturali di vibrazione devono essere 2-3 volte superiori alla frequenza di rotazione del rotore da equilibrare. Per misurare il carico di vibrazione dei supporti delle macchine di prerisonanza si utilizzano solitamente dei trasduttori di forza.
Il vantaggio delle macchine di equilibratura pre-risonanza è che su di esse l'equilibratura può essere eseguita a velocità del rotore relativamente basse (fino a 400 - 500 giri/min), il che semplifica notevolmente la progettazione della macchina e delle sue fondamenta e aumenta la produttività e la sicurezza dell'equilibratura.
Bilanciamento dei rotori rigidi
Importante!
- L'equilibratura elimina solo le vibrazioni causate dalla distribuzione asimmetrica della massa del rotore rispetto al suo asse di rotazione. Altri tipi di vibrazioni non vengono eliminati dall'equilibratura!
- I meccanismi tecnici, la cui progettazione garantisce l'assenza di risonanze alla frequenza operativa di rotazione, fissati in modo affidabile sulla fondazione, installati su cuscinetti revisionabili, sono soggetti a bilanciamento.
- I macchinari difettosi devono essere riparati prima dell'equilibratura. In caso contrario, non è possibile ottenere un'equilibratura di qualità.
L'equilibratura non sostituisce la riparazione!
Il compito principale dell'equilibratura è quello di trovare la massa e la posizione dei pesi di compensazione che sono soggetti al bilanciamento delle forze centrifughe.
Come già detto, per i rotori rigidi è generalmente necessario e sufficiente installare due pesi di compensazione. In questo modo si elimina lo squilibrio statico e dinamico del rotore. Lo schema generale per la misurazione delle vibrazioni durante l'equilibratura è il seguente.
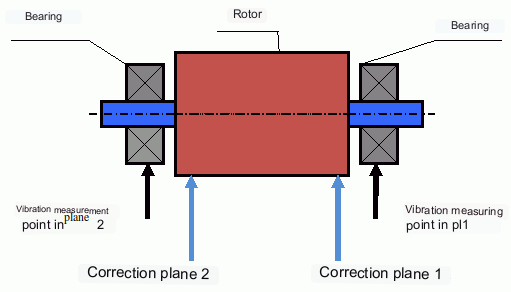
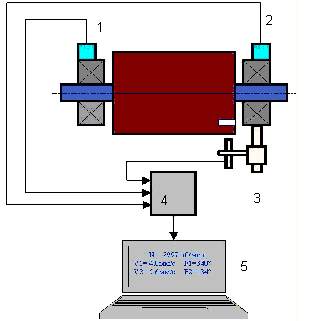
I sensori di vibrazioni sono installati sui supporti dei cuscinetti ai punti 1 e 2. Un indicatore di giri è fissato al rotore, di solito con un nastro riflettente. Il contrassegno del numero di giri viene utilizzato dal tachimetro laser per determinare la velocità del rotore e la fase del segnale di vibrazione.
Come viene eseguito il bilanciamento dinamico (metodo a tre passaggi)
Nella maggior parte dei casi l'equilibratura dinamica viene effettuata con il metodo delle tre partenze. Il metodo si basa sul fatto che i pesi di prova di peso noto vengono posizionati sul rotore in serie nei piani 1 e 2 e i pesi e la posizione dei pesi di bilanciamento vengono calcolati in base ai risultati delle variazioni dei parametri di vibrazione.
Il luogo di installazione dei pesi è chiamato piano di correzione. Di solito i piani di correzione vengono scelti nell'area dei supporti su cui è installato il rotore.
Al primo avvio si misura la vibrazione iniziale. Successivamente, un peso di prova di peso noto viene collocato sul rotore vicino a uno dei cuscinetti. Si esegue un secondo avviamento e si misurano i parametri di vibrazione, che dovrebbero cambiare a causa dell'installazione del peso di prova. Quindi il peso di prova nel primo piano viene rimosso e installato nel secondo piano. Si esegue una terza prova e si misurano i parametri di vibrazione. Il peso di prova viene rimosso e il software calcola automaticamente le masse e gli angoli di installazione dei pesi di bilanciamento.
L'installazione dei pesi di prova serve a determinare come il sistema reagisce alle variazioni di squilibrio. I pesi e le posizioni dei pesi di prova sono noti, quindi il software può calcolare i cosiddetti coefficienti di influenza, mostrando come l'introduzione di uno squilibrio noto influenzi i parametri di vibrazione. I coefficienti di influenza sono caratteristiche del sistema meccanico stesso e dipendono dalla rigidità dei supporti e dalla massa (inerzia) del sistema rotore-supporto.
Per i meccanismi dello stesso tipo e della stessa progettazione, i coefficienti di influenza saranno vicini. È possibile salvarli nella memoria del computer e utilizzarli per l'equilibratura di meccanismi dello stesso tipo senza prove, il che aumenta notevolmente la produttività dell'equilibratura. Si noti che la massa dei pesi di prova deve essere scelta in modo tale che i parametri di vibrazione cambino sensibilmente quando vengono installati i pesi di prova. In caso contrario, l'errore di calcolo dei coefficienti di influenza aumenta e la qualità dell'equilibratura peggiora.
Come si può vedere dalla Fig. 1, la forza centrifuga agisce in direzione radiale, cioè perpendicolarmente all'asse del rotore. Pertanto, i sensori di vibrazione devono essere installati in modo che anche il loro asse di sensibilità sia rivolto in direzione radiale. Di solito, la rigidità della fondazione in direzione orizzontale è minore, quindi la vibrazione in direzione orizzontale è maggiore. Pertanto, per aumentare la sensibilità, i sensori devono essere installati in modo che il loro asse di sensibilità sia diretto anche in direzione orizzontale. Anche se non c'è una differenza fondamentale. Oltre alle vibrazioni in direzione radiale, è necessario monitorare le vibrazioni in direzione assiale, lungo l'asse di rotazione del rotore. Questa vibrazione di solito non è causata dallo sbilanciamento, ma da altre cause, principalmente legate al disallineamento e al disassamento degli alberi collegati attraverso il giunto.
Questa vibrazione non può essere eliminata tramite bilanciamento, nel qual caso è necessario l'allineamento. In pratica, tali macchine presentano solitamente sia uno sbilanciamento del rotore che un disallineamento dell'albero, il che rende molto più difficile l'eliminazione delle vibrazioni. In questi casi, è necessario prima centrare la macchina e poi bilanciarla. (Sebbene in caso di forte sbilanciamento della coppia, le vibrazioni si verifichino anche in direzione assiale a causa della "torsione" della struttura di fondazione.)
Articoli correlati (esempi di supporti di bilanciamento)
- Supporto di bilanciamento con supporto morbido
- Bilanciamento dei rotori dei motori elettrici
- Cavalletti di bilanciamento semplici ma efficaci
Criteri per la valutazione della qualità dei meccanismi di bilanciamento
La qualità del bilanciamento dei rotori (meccanismi) può essere valutata in due modi. Il primo metodo consiste nel confrontare l'entità dello squilibrio residuo determinato durante il processo di equilibratura con la tolleranza per lo squilibrio residuo. Queste tolleranze per le diverse classi di rotori sono specificate nella norma ISO 1940-1-2007. Parte 1. Definizione di squilibrio ammissibile.
Tuttavia, il rispetto delle tolleranze specificate non può garantire pienamente l'affidabilità operativa del meccanismo, associata al raggiungimento del livello minimo di vibrazioni. Ciò si spiega con il fatto che l'entità delle vibrazioni del meccanismo è determinata non solo dall'entità della forza associata allo squilibrio residuo del suo rotore, ma dipende anche da diversi altri parametri, tra cui: la rigidità k degli elementi strutturali del meccanismo, la sua massa m, il fattore di smorzamento e la frequenza di rotazione. Pertanto, per stimare le qualità dinamiche del meccanismo (compresa la qualità del suo equilibrio) in molti casi si raccomanda di stimare il livello di vibrazione residua del meccanismo, che è regolato da una serie di norme.
Lo standard più comune, che regola i livelli ammissibili di vibrazione dei meccanismi, è l'ISO 10816-3-2002. Con il suo aiuto, è possibile stabilire le tolleranze per qualsiasi tipo di macchina, tenendo conto della potenza del suo azionamento elettrico.
Oltre a questo standard universale, esiste una serie di standard specializzati sviluppati per tipi specifici di macchine. Ad esempio, 31350-2007, ISO 7919-1-2002, ecc.
Standard e riferimenti
- ISO 1940-1:2007. Vibrazioni. Requisiti per la qualità dell'equilibratura dei rotori rigidi. Parte 1. Determinazione dello squilibrio ammissibile.
- Norma ISO 10816-3:2009. Vibrazioni meccaniche — Valutazione delle vibrazioni della macchina mediante misurazioni su parti non rotanti — Parte 3: Macchine industriali con potenza nominale superiore a 15 kW e velocità nominali comprese tra 120 giri/min e 15.000 giri/min quando misurate in situ.
- ISO 14694:2003. Ventilatori industriali — Specifiche per la qualità dell'equilibrio e i livelli di vibrazione.
- ISO 7919-1:2002. Vibrazioni delle macchine senza moto alternativo — Misurazioni sugli alberi rotanti e criteri di valutazione — Indicazioni generali.
FAQ
L'equilibratura elimina tutte le vibrazioni?
No. L'equilibratura elimina le vibrazioni causate dalla distribuzione asimmetrica della massa del rotore rispetto al suo asse di rotazione. Le vibrazioni dovute a disallineamento, difetti dei cuscinetti, forze aerodinamiche/idrodinamiche, forze elettromagnetiche e altre cause richiedono diagnosi e azioni correttive separate.
Perché il bilanciamento può fallire in prossimità della risonanza?
In prossimità della risonanza, piccole variazioni di velocità possono causare grandi variazioni nell'ampiezza delle vibrazioni e uno sfasamento di 180°. In tali condizioni, i risultati delle misurazioni diventano instabili e le procedure di bilanciamento convenzionali potrebbero non convergere senza metodi speciali.
Quando è necessario il bilanciamento su un piano o su due piani?
Per un rotore rigido, due pesi separati lungo la sua lunghezza sono generalmente necessari e sufficienti per eliminare lo squilibrio combinato statico e dinamico. I rotori stretti spesso presentano principalmente squilibrio statico, ma la deformazione e la geometria possono introdurre una componente dinamica che potrebbe richiedere una correzione su due piani.
Cosa bisogna fare prima di effettuare il bilanciamento?
Assicurarsi che la macchina sia in condizioni di manutenzione: montaggio affidabile alla fondazione, cuscinetti in buone condizioni, assenza di allentamenti gravi e assenza di evidenti fonti di non linearità. L'equilibratura non sostituisce la riparazione.
Punti chiave
- Il bilanciamento corregge l'eccitazione correlata alla massa (centrifuga); non risolve il disallineamento, i danni ai cuscinetti o le fonti elettromagnetiche/aerodinamiche.
- La risonanza e la non linearità possono rendere il bilanciamento convenzionale inefficace o pericoloso.
- Per i rotori rigidi, l'equilibratura su due piani è la soluzione generale per lo squilibrio combinato statico + dinamico.






