Balansiranje rotora: statička i dinamička neravnoteža, rezonancija i praktični postupak
Ovaj vodič objašnjava balansiranje rotora za kruti rotorišto znači “neravnoteža”, kako se razlikuju statička i dinamička neravnoteža, zašto rezonancija i nelinearnost mogu spriječiti kvalitetan rezultat i kako se balansiranje obično izvodi u jednoj ili dvije korekcijske ravnine.
Sadržaj
- Što je rotor i što ispravlja balansiranje?
- Vrste rotora i vrste neravnoteže
- Vibracije mehanizama: što balansiranje može, a što ne može ukloniti
- Rezonancija: faktor koji sprječava uravnoteženje
- Linearni i nelinearni modeli: kada izračuni prestanu raditi
- Balancing devices and balancing machines
- Balansiranje krutih rotora (praktične napomene)
- Kako se izvodi dinamičko balansiranje (metoda s tri prolaza)
- Kriteriji za procjenu kvalitete uravnoteženja
- Standardi i reference
- FAQ
Što je rotor i što ispravlja balansiranje?
The rotor is a body which rotates about some axis and is held by its bearing surfaces in the supports. The bearing surfaces of the rotor transmit loads to the supports via rolling or sliding bearings. The bearing surfaces are the surfaces of the trunnions or the surfaces that replace them.
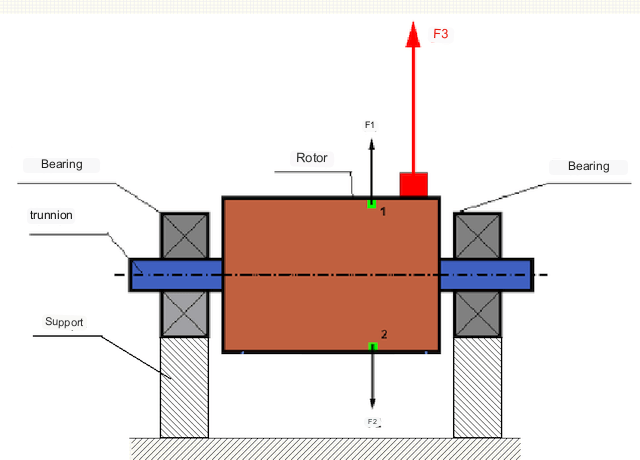
U savršeno uravnoteženom rotoru, njegova masa je simetrično raspoređena oko osi rotacije, tj. bilo koji element rotora može se uskladiti s drugim elementom koji se nalazi simetrično oko osi rotacije. U uravnoteženom rotoru, centrifugalna sila koja djeluje na bilo koji element rotora uravnotežena je centrifugalnom silom koja djeluje na simetrični element. Na primjer, centrifugalne sile F1 i F2, jednake veličine i suprotnog smjera, djeluju na elemente 1 i 2 (označeni zelenom bojom na slici 1). To vrijedi za sve simetrične elemente rotora, te je stoga ukupna centrifugalna sila koja djeluje na rotor jednaka 0 i rotor je uravnotežen.
Ali ako je simetrija rotora narušena (asimetrični element je označen crvenom bojom na Sl. 1), tada na rotor djeluje neuravnotežena centrifugalna sila F3. Prilikom rotacije, ta sila mijenja smjer s rotacijom rotora. Dinamičko opterećenje koje nastaje zbog ove sile prenosi se na ležajeve, što rezultira ubrzanim trošenjem.
In addition, under the influence of this variable in direction force there is a cyclic deformation of supports and foundation, on which the rotor is fixed, i.e. there is vibration. In order to eliminate rotor imbalance and the accompanying vibration, balancing masses must be installed to restore symmetry to the rotor.
Rotor balancing is an operation to correct imbalance by adding balancing masses.
The task of balancing is to find the size and location (angle) of one or more balancing masses.
Vrste rotora i vrste neravnoteže
Uzimajući u obzir čvrstoću materijala rotora i veličinu centrifugalnih sila koje na njega djeluju, rotori se mogu podijeliti u dvije vrste - krute rotore i fleksibilne rotore.
Rigid rotors deform insignificantly under action of centrifugal force at working modes and influence of this deformation in calculations can be neglected.
Deformacija fleksibilnih rotora više se ne može zanemariti. Deformacija fleksibilnih rotora komplicira rješavanje problema balansiranja i zahtijeva primjenu drugih matematičkih modela u usporedbi s problemom balansiranja krutih rotora. Treba napomenuti da se isti rotor pri malim brzinama može ponašati kao krut, a pri velikim brzinama kao fleksibilan. U nastavku ćemo razmatrati samo balansiranje krutih rotora.
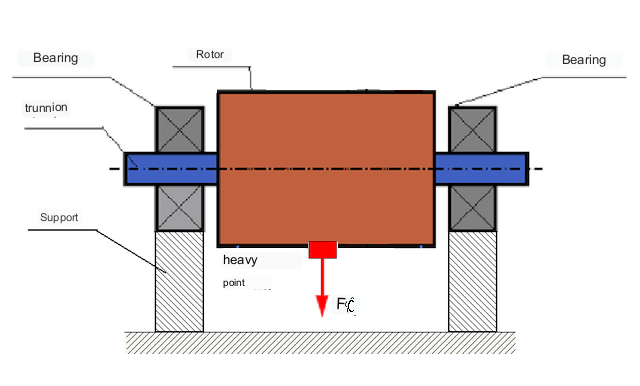
Ovisno o raspodjeli neuravnoteženih masa duž duljine rotora, mogu se razlikovati dvije vrste neuravnoteženosti - statička i dinamička (trenutna). Sukladno tome, nazivaju se statička i dinamička uravnoteženost rotora. Statička neuravnoteženost rotora nastaje bez rotacije rotora, tj. u statici, kada se rotor gravitacijom okreće s "težom točkom" prema dolje. Primjer rotora sa statičkom neuravnoteženošću prikazan je na slici 2.
Dynamic unbalance occurs only when the rotor is rotating.
An example of a rotor with dynamic unbalance is shown in Fig. 3.
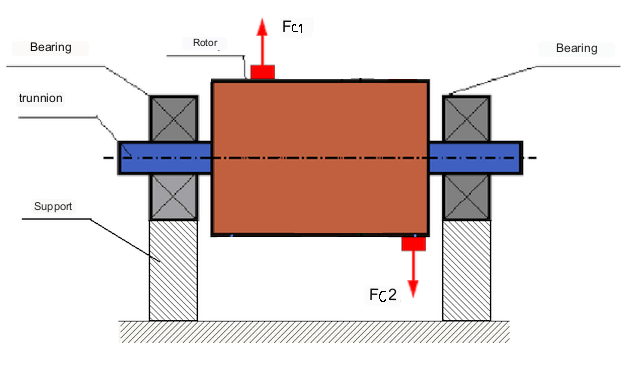
U ovom slučaju, neuravnotežene jednake mase M1 i M2 nalaze se u različitim ravninama - na različitim mjestima duž duljine rotora. U statičkom položaju, tj. kada se rotor ne okreće, na rotor djeluje samo gravitacija, a mase se međusobno uravnotežuju. U dinamici, kada se rotor okreće, na mase M1 i M2 počinju djelovati centrifugalne sile Fc1 i Fc2. Ove sile su jednake veličine i suprotnog smjera. Međutim, budući da se primjenjuju na različitim mjestima duž duljine osovine i nisu na istoj liniji, ove se sile međusobno ne kompenziraju. Sile Fc1 i Fc2 stvaraju moment koji se primjenjuje na rotor. Stoga se ovaj neravnotež naziva i moment neravnoteže. Sukladno tome, na položaje ležajeva djeluju nekompenzirane centrifugalne sile, koje mogu znatno premašiti izračunate vrijednosti i smanjiti vijek trajanja ležajeva.
Budući da se ova vrsta neravnoteže javlja samo dinamički tijekom rotacije rotora, naziva se dinamička neravnoteža. Ne može se ispraviti u statičkim uvjetima balansiranjem "na noževima" ili sličnim metodama. Kako bi se uklonila dinamička neravnoteža, moraju se ugraditi dvije kompenzacijske težine koje proizvode moment jednake veličine i suprotnog smjera od momenta koji proizlazi iz masa M1 i M2. Kompenzacijske mase ne moraju biti postavljene nasuprot i jednake veličine masama M1 i M2. Glavno je da proizvode moment koji u potpunosti kompenzira moment neravnoteže.
Općenito, mase M1 i M2 ne moraju biti jednake, pa će postojati kombinacija statičke i dinamičke neravnoteže. Teoretski je dokazano da su za kruti rotor dva utega razmaknuta duž duljine rotora potrebna i dovoljna za uklanjanje njegove neravnoteže. Ovi utezi će kompenzirati i moment koji nastaje zbog dinamičke neravnoteže i centrifugalnu silu koja nastaje zbog asimetrije mase u odnosu na os rotora (statička neravnoteža). Tipično, dinamička neravnoteža je karakteristična za duge rotore, poput osovina, a statička neravnoteža je karakteristična za uske rotore. Međutim, ako je uski rotor iskrivljen u odnosu na os ili deformiran ("osmica"), tada će dinamičku neravnotežu biti teško ukloniti (vidi sliku 4), jer je u tom slučaju teško ugraditi korektivne utege koji stvaraju potreban kompenzacijski moment.
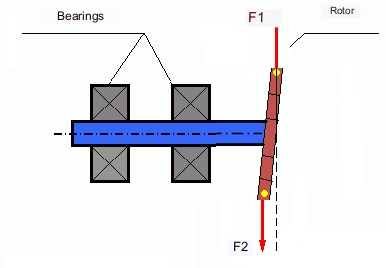
The forces F1 and F2 do not lie on the same line and do not compensate each other.
Zbog činjenice da je krak za stvaranje momenta malen zbog uskog rotora, mogu biti potrebni veliki korekcijski utezi. Međutim, to također rezultira "induciranom neravnotežom" zbog deformacije uskog rotora centrifugalnim silama od korekcijskih utega. (Vidi na primjer "Metodološke upute za balansiranje krutih rotora (prema ISO 22061-76)". Odjeljak 10. SUSTAV NOSAČA ROTORA.)
This is noticeable for narrow impellers of fans, in which, in addition to force unbalance, aerodynamic unbalance is also active. And it should be understood that aerodynamic unbalance, or rather aerodynamic force is directly proportional to angular speed of the rotor, and for its compensation the centrifugal force of correcting mass, which is proportional to the square of angular speed, is used. Therefore, the balancing effect can only take place at a specific balancing frequency. At other rotational frequencies there is an additional error.
The same can be said of the electromagnetic forces in an electric motor, which are also proportional to angular velocity. So it is not possible to eliminate all causes of vibration in a machine by balancing.
Vibracije mehanizama
Vibration is the reaction of the mechanism design to the effects of a cyclic excitatory force. This force can be of different nature.
Centrifugalna sila koja nastaje zbog neuravnoteženog rotora je nekompenzirana sila koja djeluje na "tešku točku". Upravo se ta sila i vibracije uzrokovane njome mogu eliminirati uravnoteženjem rotora.
Interakcijske sile "geometrijske" prirode koje proizlaze iz pogrešaka u proizvodnji i montaži spojnih dijelova. Ove sile mogu, na primjer, nastati kao rezultat nekružnosti vratova vratila, pogrešaka u profilima zuba u zupčanicima, valovitosti staza ležajeva, neusklađenosti spojnih vratila itd. U slučaju nekružnosti rukavaca, os vratila će se pomaknuti ovisno o kutu rotacije vratila. Iako se ova vibracija javlja i pri brzini rotora, gotovo ju je nemoguće eliminirati balansiranjem.
Aerodynamic forces resulting from the rotation of the impellers of fans and other vane mechanisms. Hydrodynamic forces resulting from the rotation of impellers of hydraulic pumps, turbines, etc.
Electromagnetic forces resulting from the operation of electrical machines, e.g. asymmetric rotor windings, short-circuited windings, etc.
The magnitude of the vibration (e.g. its amplitude Av) depends not only on the excitatory force Fv acting on the mechanism with circular frequency ω, but also on the rigidity k of the mechanism, its mass m , as well as the damping coefficient C.
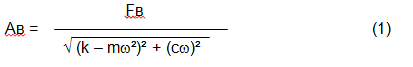
Various types of sensors can be used to measure vibration and balance mechanisms, including:
- absolute vibration sensors designed to measure vibration acceleration (accelerometers) and vibration velocity sensors;
- senzori relativnih vibracija - vrtložne struje ili kapacitivni, dizajnirani za mjerenje pomaka vibracija;
- U nekim slučajevima (kada to dizajn mehanizma dopušta), senzori sile mogu se koristiti i za procjenu njegovog vibracijskog opterećenja; posebno se široko koriste za mjerenje vibracijskog opterećenja nosača strojeva za balansiranje s tvrdim ležajevima.
So, vibration is the reaction of a machine to the action of external forces. The magnitude of vibration depends not only on the magnitude of the force acting on the mechanism, but also on the rigidity of the mechanism design. One and the same force can lead to different vibrations. In a hard-bearing machine, even if the vibration is small, the bearings may be subjected to significant dynamic loads. This is why force rather than vibration sensors (vibration accelerometers) are used when balancing hard-bearing machines.
Vibration sensors are used on mechanisms with relatively pliable supports, when the action of unbalanced centrifugal forces leads to a noticeable deformation of supports and vibration. Force sensors are used for rigid supports, when even significant forces due to unbalance do not lead to significant vibration.
Resonance is a factor that prevents balancing
Earlier we mentioned that rotors are divided into rigid and flexible. Stiffness or flexibility of rotor should not be confused with stiffness or mobility of supports (foundation) on which the rotor is installed. A rotor is considered rigid when its deformation (bending) under the action of centrifugal forces can be neglected. Deformation of flexible rotor is relatively large and cannot be neglected.
In this article, we consider only the balancing of rigid rotors. A rigid (non-deformable) rotor can in turn be mounted on rigid or movable (pliable) supports. It is clear that this stiffness/suspendability of supports is also relative, depending on rotor speed and magnitude of resulting centrifugal forces. A conditional boundary is the frequency of natural vibrations of the rotor supports.
For mechanical systems, the shape and frequency of natural vibrations are determined by the mass and the elasticity of the elements of mechanical system. That is, the frequency of natural vibrations is an internal characteristic of the mechanical system and does not depend on external forces. Being deflected from the state of equilibrium, supports due to elasticity tend to return to the position of equilibrium. But due to the inertia of the massive rotor, this process is in the nature of damped oscillations. These vibrations are the natural vibrations of the rotor-support system. Their frequency depends on the ratio of the mass of the rotor to the elasticity of the supports.
When the rotor begins to rotate and the frequency of its rotation approaches the frequency of natural vibrations, the amplitude of vibration increases sharply, which can lead to the destruction of the structure.
The phenomenon of mechanical resonance occurs. In the area of resonance, a change of rotation speed by 100 rpm may lead to an increase in vibration by tens of times. At the same time (in the resonance area) the vibration phase changes by 180°.
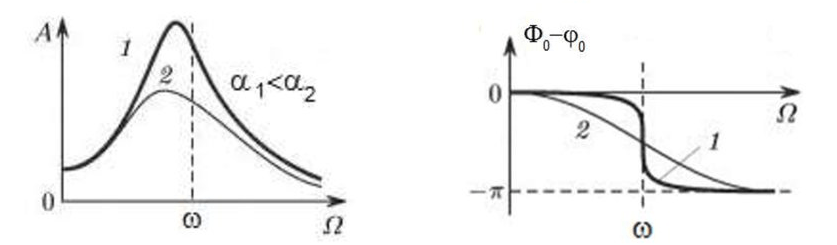
If the design of the mechanism is unsuccessful and the operating frequency of the rotor is close to the frequency of natural vibrations, then the operation of the mechanism becomes impossible because of the inadmissibly high vibration. This is not possible in the usual way, since even a small change in speed will cause a drastic change in the vibration parameters. For balancing in the area of resonance, special methods not considered in this article are used.
It is possible to determine the frequency of natural vibrations of the mechanism at coasting (at switching off the rotor rotation) or by the shock method with the subsequent spectral analysis of the system response to the shock.
For mechanisms, which working frequency of rotation is above the resonance frequency, i.e. working in the resonance regime, the supports are considered to be moving and for measurement are used vibration sensors, mainly vibroacelerometers, measuring acceleration of structural elements. For mechanisms operating in preresonant mode, the supports are considered rigid. In this case, force sensors are used.
Linear and nonlinear models of a mechanical system. Non-linearity is a factor that prevents balancing
When balancing rigid rotors, mathematical models called linear models are used for balancing calculations. A linear model means that in such a model, one quantity is proportional (linear) to the other. For example, if the uncompensated mass on the rotor is doubled, then the vibration value will also be doubled. For rigid rotors, a linear model can be used, since they do not deform.
For flexible rotors, the linear model can no longer be used. For a flexible rotor, if the mass of the heavy point increases during rotation, additional deformation will occur, and in addition to the mass, the radius of the location of the heavy point will also increase. Therefore, for a flexible rotor, the vibration will increase more than twofold, and the usual methods of calculation will not work.
Also, the change of elasticity of supports at their large deformations, for example, when at small deformations of supports some structural elements work, and at large ones other structural elements are involved. This is why you cannot balance mechanisms that are not fixed on a foundation, but, for example, simply placed on the floor. With significant vibrations, the force of the imbalance can pull the mechanism off the floor, thereby significantly changing the stiffness characteristics of the system. Motor feet must be securely fastened, bolt mounts must be tightened, washer thickness must provide sufficient mounting rigidity, etc. If the bearings are broken, significant shaft misalignment and shocks are possible, which will also result in poor linearity and an inability to perform a quality balance.
Balancing devices and balancing machines
Kao što je gore navedeno, balansiranje je proces poravnavanja glavne središnje osi inercije s osi rotacije rotora.
This process can be performed by two methods.
The first method involves machining the rotor trunnions in such a way that the axis passing through the centers of the trunnions cross section with the main central axis of inertia of the rotor. Such a technique is rarely used in practice and will not be discussed in detail in this article.
The second (most common) method involves moving, installing or removing correction weights on the rotor, which are placed so that the axis of inertia of the rotor is as close to its axis of rotation as possible.
Moving, adding or removing correction weights during balancing may be accomplished by various technological operations including: drilling, milling, surfacing, welding, screwing or unscrewing, laser or electron beam burning, electrolysis, electromagnetic surfacing, etc.
The balancing process can be accomplished in two ways:
- balancing of assembled rotors (in their own bearings) using balancing machines;
- balancing of rotors on balancing machines. For balancing of rotors in their own bearings usually used specialized balancing devices (kits), which allow to measure the vibration of the balanced rotor at its frequency of rotation in vector form, i.e. to measure both the amplitude and the phase of vibration. At present, the above devices are manufactured on the basis of microprocessor technology and (apart from vibration measurement and analysis) provide automatic calculation of parameters of correcting weights, which should be installed on the rotor to compensate its unbalance.
These devices include:
- a measuring and computing unit based on a computer or industrial controller;
- Two (or more) vibration sensors;
- A phase angle sensor;
- accessories for mounting the sensors on the site;
- specialized software, designed to perform a full cycle of rotor vibration parameters measurement in one, two or more correction planes.
Two types of balancing machines are currently the most common:
- Soft-bearings machines (with soft supports);
- Hard-bearings machines (with rigid supports).
Strojevi s mekim ležajevima imaju relativno savitljive nosače, na primjer, na bazi ravnih opruga. Frekvencija vlastitih vibracija tih nosača obično je 2-3 puta niža od frekvencije vrtnje balansirajućeg rotora, koji je na njima montiran. Senzori vibracija (akcelerometri, senzori brzine vibracija itd.) obično se koriste pri mjerenju vibracija predrezonantnih nosača stroja.
Pre-resonance balancing machines use relatively rigid supports, whose natural frequencies of vibration should be 2-3 times higher than the rotation frequency of the rotor being balanced. Force transducers are usually used to measure the vibration load of the preresonance machine supports.
Prednost strojeva za predrezonantno balansiranje je u tome što se balansiranje na njima može izvoditi pri relativno niskim brzinama rotora (do 400 - 500 o/min), što uvelike pojednostavljuje dizajn stroja i njegovog temelja te povećava produktivnost i sigurnost balansiranja.
Balancing rigid rotors
Važno!
- Balancing only eliminates vibration caused by asymmetrical distribution of the rotor mass relative to its rotational axis. Other types of vibration are not eliminated by balancing!
- Technical mechanisms, whose design ensures the absence of resonances at the operating frequency of rotation, reliably fixed on the foundation, installed in serviceable bearings, are subject to balancing.
- Defective machinery must be repaired before balancing. Otherwise, quality balancing is not possible.
Balancing is no substitute for repair!
The main task of balancing is to find the mass and location of compensating weights that are subject to balancing centrifugal forces.
As mentioned above, for rigid rotors, it is generally necessary and sufficient to install two compensating weights. This will eliminate both static and dynamic unbalance of the rotor. The general scheme for measuring vibration during balancing is as follows.
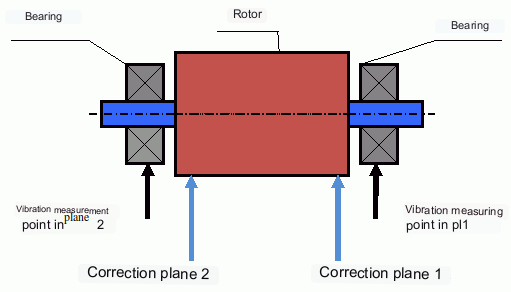
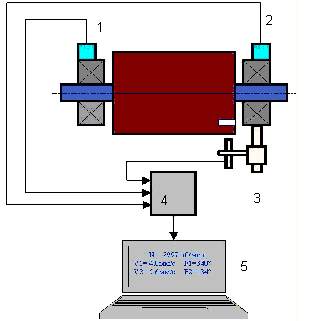
Vibration sensors are installed on the bearing supports at points 1 and 2. A revolution marker is attached to the rotor, usually with reflective tape. The RPM mark is used by the laser tachometer to determine the rotor speed and phase of the vibration signal.
Kako se izvodi dinamičko balansiranje (metoda s tri prolaza)
In most cases dynamic balancing is carried out by the method of three starts. The method is based on the fact that test weights of known weight are placed on the rotor in series in plane 1 and 2 and the weights and the location of the balancing weights are calculated based on the results of changes in the vibration parameters.
The place of installation of weights is called the correction plane. Usually the correction planes are selected in the area of the bearing supports on which the rotor is installed.
At the first start-up the initial vibration is measured. Then a test weight of known weight is placed on the rotor closer to one of the bearings. A second start-up is carried out and the vibration parameters are measured, which should change due to the test weight installation. Then the test weight in the first plane is removed and installed in the second plane. A third test run is performed and the vibration parameters are measured. The test weight is removed and the software automatically calculates the masses and installation angles of the balance weights.
The point of installing the test weights is to determine how the system reacts to changes in imbalance. The weights and locations of the test weights are known, so the software can calculate so called influence coefficients, showing how introducing a known imbalance affects the vibration parameters. The influence coefficients are characteristics of the mechanical system itself and depend on the rigidity of the supports and the mass (inertia) of the rotor-support system.
For the same type of mechanisms of the same design the influence coefficients will be close. It is possible to save them in the computer memory and use them for balancing of the same-type mechanisms without test runs, which significantly increases the productivity of balancing. Note that the mass of test weights should be chosen such that the vibration parameters change noticeably when test weights are installed. Otherwise, the error of calculation of influence coefficients increases and the quality of balancing deteriorates.
As you can see from Fig. 1, the centrifugal force acts in the radial direction, i.e. perpendicular to the rotor axis. Therefore, the vibration sensors must be installed so that their axis of sensitivity also points in the radial direction. Usually, the stiffness of the foundation in the horizontal direction is less, so the vibration in the horizontal direction is higher. Therefore, in order to increase the sensitivity, the sensors should be installed so that their axis of sensitivity is also directed horizontally. Although there is no fundamental difference. In addition to vibration in the radial direction, vibration in the axial direction, along the rotor rotation axis, must be monitored. This vibration is usually not caused by unbalance, but by other causes, mainly related to misalignment and misalignment of the shafts connected through the coupling.
Ova vibracija se ne može ukloniti balansiranjem, u kojem slučaju je potrebno poravnanje. U praksi, takvi strojevi obično imaju i neravnotežu rotora i neusklađenost osovine, što znatno otežava zadatak uklanjanja vibracija. U takvim slučajevima potrebno je prvo centrirati stroj, a zatim ga balansirati. (Iako se kod jakog neravnoteže momenta vibracije javljaju i u aksijalnom smjeru zbog "uvijanja" temeljne konstrukcije.)
Povezani članci (primjeri balansirajućih postolja)
- Stalak za balansiranje s mekom potporom
- Balansiranje rotora elektromotora
- Simple but effective balancing stands
Kriteriji za procjenu kvalitete mehanizama uravnoteženja
The balancing quality of rotors (mechanisms) can be evaluated in two ways. The first method involves comparing the amount of residual unbalance determined during the balancing process with the tolerance for residual unbalance. These tolerances for the different rotor classes are specified in ISO 1940-1-2007. Part 1. Definition of allowable unbalance.
However, compliance with the specified tolerances cannot fully guarantee the operational reliability of the mechanism, associated with the achievement of the minimum level of its vibration. This is explained by the fact that the magnitude of vibration of the mechanism is determined not only by the magnitude of the force associated with the residual unbalance of its rotor, but also depends on several other parameters, including: the rigidity k of the mechanism structural elements, its mass m, the damping factor, as well as the rotation frequency. Therefore, to estimate dynamic qualities of the mechanism (including quality of its balance) in a number of cases it is recommended to estimate the level of residual vibration of the mechanism, which is regulated by a number of standards.
The most common standard, which regulates the admissible levels of vibration of mechanisms is ISO 10816-3-2002. With its help, it is possible to set tolerances for any type of machines, taking into account the power of their electric drive.
In addition to this universal standard, there is a number of specialized standards developed for specific types of machines. For example, 31350-2007 , ISO 7919-1-2002, etc.
Standardi i reference
- ISO 1940-1:2007. Vibracije. Zahtjevi za kvalitetu uravnoteženja krutih rotora. Dio 1. Određivanje dopuštene neravnoteže.
- ISO 10816-3:2009. Mehaničke vibracije — Procjena vibracija strojeva mjerenjima na nerotirajućim dijelovima — Dio 3: Industrijski strojevi nazivne snage iznad 15 kW i nazivnih brzina između 120 o/min i 15 000 o/min pri mjerenju na licu mjesta.
- ISO 14694:2003. Industrijski ventilatori — Specifikacije za kvalitetu uravnoteženja i razinu vibracija.
- ISO 7919-1:2002. Vibracije strojeva bez povratnog gibanja — Mjerenja na rotirajućim osovinama i kriteriji procjene — Opće smjernice.
FAQ
Uklanja li balansiranje sve vibracije?
Ne. Balansiranje uklanja vibracije uzrokovane asimetričnom raspodjelom mase rotora u odnosu na njegovu rotacijsku os. Vibracije uzrokovane neusklađenošću, nedostacima ležajeva, aerodinamičkim/hidrodinamičkim silama, elektromagnetskim silama i drugim uzrocima zahtijevaju zasebnu dijagnostiku i korektivne radnje.
Zašto balansiranje može propasti blizu rezonancije?
Blizu rezonancije, male promjene brzine mogu uzrokovati velike promjene amplitude vibracija i fazni pomak od 180°. U takvim uvjetima rezultati mjerenja postaju nestabilni, a konvencionalni postupci balansiranja možda neće konvergirati bez posebnih metoda.
Kada vam je potrebno balansiranje u jednoj ravnini u odnosu na balansiranje u dvije ravnine?
Za kruti rotor, dvije težine razdvojene duž duljine rotora općenito su potrebne i dovoljne za uklanjanje kombinirane statičke i dinamičke neravnoteže. Uski rotori često pokazuju uglavnom statičku neravnotežu, ali deformacija i geometrija mogu uvesti dinamičku komponentu koja može zahtijevati korekciju u dvije ravnine.
Što treba učiniti prije balansiranja?
Provjerite je li stroj ispravan: pouzdano pričvršćivanje na temelj, ispravni ležajevi, bez ozbiljnih labavosti i bez očitih izvora nelinearnosti. Balansiranje nije zamjena za popravak.
Ključne zaključke
- Balansiranjem se ispravlja uzbuđenje povezano s masom (centrifugalno); ne rješava se problem neusklađenosti, oštećenja ležajeva ili elektromagnetskih/aerodinamičkih izvora.
- Rezonancija i nelinearnost mogu učiniti konvencionalno balansiranje neučinkovitim ili nesigurnim.
- Za krute rotore, dvoravninsko balansiranje je opće rješenje za kombiniranu statičku i dinamičku neravnotežu.






