Rotorbalansering: statisk och dynamisk obalans, resonans och praktisk procedur
Den här guiden förklarar rotorbalansering för styva rotorer: vad "obalans" betyder, hur statisk och dynamisk obalans skiljer sig åt, varför resonans och icke-linjäritet kan förhindra ett kvalitetsresultat, och hur balansering vanligtvis utförs i ett eller två korrektionsplan.
Innehåll
- Vad är en rotor och vad korrigerar balanseringen?
- Typer av rotorer och typer av obalans
- Vibrationer i mekanismer: vad balansering kan och inte kan ta bort
- Resonans: en faktor som förhindrar balansering
- Linjära kontra icke-linjära modeller: när beräkningar slutar fungera
- Balanseringsanordningar och balanseringsmaskiner
- Balansering av stela rotorer (praktiska anteckningar)
- Hur dynamisk balansering utförs (trestegsmetoden)
- Kriterier för bedömning av balanseringskvalitet
- Standarder och referenser
- VANLIGA FRÅGOR
Vad är en rotor och vad korrigerar balanseringen?
Rotorn är en kropp som roterar runt en axel och hålls fast av sina lagerytor i stöden. Rotorns lagerytor överför belastningar till stöden via rull- eller glidlager. Lagerytorna är ytorna på tapparna eller de ytor som ersätter dem.
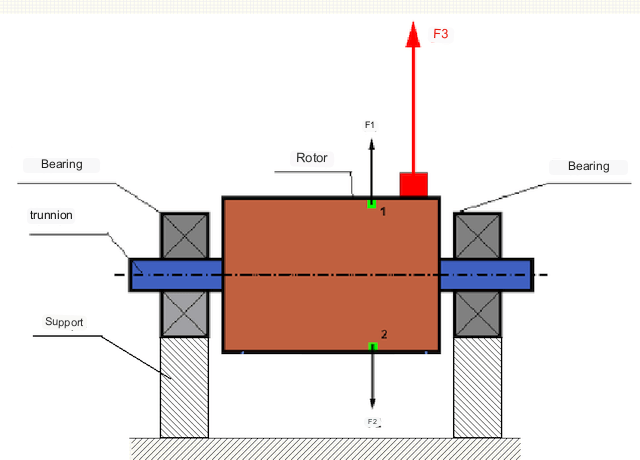
I en perfekt balanserad rotor är dess massa symmetriskt fördelad kring rotationsaxeln, dvs. vilket element som helst i rotorn kan matchas med ett annat element som är placerat symmetriskt kring rotationsaxeln. I en balanserad rotor balanseras centrifugalkraften som verkar på vilket rotorelement som helst av centrifugalkraften som verkar på det symmetriska elementet. Till exempel verkar centrifugalkrafterna F1 och F2, lika stora och motsatt riktade, på elementen 1 och 2 (markerade med grönt i figur 1). Detta gäller för alla symmetriska rotorelement, och därmed är den totala centrifugalkraften som verkar på rotorn 0 och rotorn är balanserad.
Men om rotorns symmetri bryts (asymmetriskt element markeras med rött i figur 1), verkar en obalanserad centrifugalkraft F3 på rotorn. Vid rotation ändrar denna kraft riktning med rotorns rotation. Den dynamiska belastningen som härrör från denna kraft överförs till lagren, vilket resulterar i accelererat slitage.
Under påverkan av denna variabla riktningskraft uppstår dessutom en cyklisk deformation av stöd och fundament, på vilka rotorn är fixerad, dvs. det uppstår vibrationer. För att eliminera rotorobalansen och de medföljande vibrationerna måste balanseringsmassor installeras för att återställa symmetrin i rotorn.
Rotorbalansering är ett ingrepp för att korrigera obalans genom att tillföra balanseringsmassor.
Balanseringens uppgift är att hitta storlek och läge (vinkel) för en eller flera balansmassor.
Typer av rotorer och typer av obalans
Med hänsyn till rotormaterialets hållfasthet och storleken på de centrifugalkrafter som verkar på det kan rotorer delas in i två typer - styva rotorer och flexibla.
Styva rotorer deformeras obetydligt under inverkan av centrifugalkraften i arbetslägen och påverkan av denna deformation i beräkningarna kan försummas.
Deformation av flexibla rotorer kan inte längre försummas. Deformation av flexibla rotorer komplicerar lösningen av balanseringsproblemet och kräver tillämpning av andra matematiska modeller i jämförelse med problemet med balansering av styva rotorer. Det bör noteras att samma rotor vid låga hastigheter kan bete sig som styv, och vid höga hastigheter - som flexibel. I det följande kommer vi endast att behandla balansering av styva rotorer.
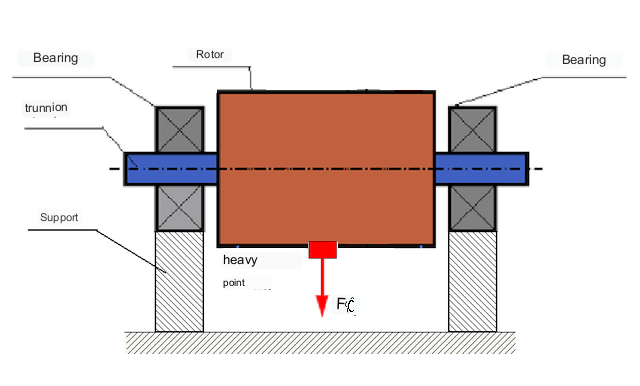
Beroende på fördelningen av obalanserade massor längs rotorns längd kan två typer av obalans urskiljas - statisk och dynamisk (momentan). Följaktligen avses statisk och dynamisk rotorbalansering. Statisk rotorobalans uppstår utan rotation av rotorn, dvs. i statik, när rotorn reverseras av gravitationen med sin "tunga punkt" nedåt. Ett exempel på en rotor med statisk obalans visas i figur 2.
Dynamisk obalans uppstår endast när rotorn roterar.
Ett exempel på en rotor med dynamisk obalans visas i fig. 3.
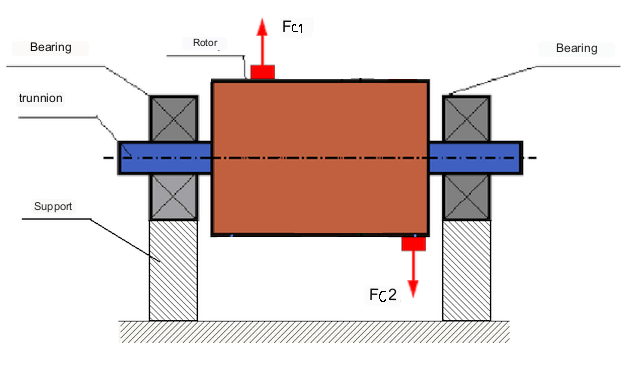
I detta fall befinner sig de obalanserade, lika stora massorna M1 och M2 i olika plan - på olika platser längs rotorns längd. I statiskt läge, dvs. när rotorn inte roterar, verkar endast gravitationen på rotorn och massorna balanserar varandra. I dynamik, när rotorn roterar, börjar centrifugalkrafterna Fc1 och Fc2 verka på massorna M1 och M2. Dessa krafter är lika stora och motsatt riktade. Men eftersom de appliceras på olika platser längs axelns längd och inte ligger på samma linje, kompenserar dessa krafter inte varandra. Krafterna Fc1 och Fc2 skapar ett vridmoment som appliceras på rotorn. Därför kallas denna obalans även momentobalans. Följaktligen verkar okompenserade centrifugalkrafter på lagerpositionerna, vilket kan överstiga de beräknade värdena avsevärt och minska lagrens livslängd.
Eftersom denna typ av obalans endast uppstår dynamiskt under rotorns rotation kallas den dynamisk obalans. Den kan inte korrigeras under statiska förhållanden genom balansering "på knivar" eller liknande metoder. För att eliminera dynamisk obalans måste två kompensationsvikter installeras, vilka producerar ett moment som är lika stort och motsatt riktat som det moment som uppstår från massorna M1 och M2. De kompenserande massorna behöver inte placeras motsatt och lika stort som massorna M1 och M2. Det viktigaste är att de producerar ett moment som helt kompenserar för obalansmomentet.
Generellt sett kan massorna M1 och M2 vara ojämna, så det kommer att finnas en kombination av statisk och dynamisk obalans. Det är teoretiskt bevisat att för en stel rotor är två vikter placerade längs rotorns längd nödvändiga och tillräckliga för att eliminera dess obalans. Dessa vikter kompenserar både vridmomentet som härrör från dynamisk obalans och centrifugalkraften som härrör från massans asymmetrin i förhållande till rotoraxeln (statisk obalans). Vanligtvis är dynamisk obalans karakteristisk för långa rotorer, såsom axlar, och statisk obalans är karakteristisk för smala rotorer. Men om den smala rotorn är sned i förhållande till axeln, eller deformerad ("figur åtta"), kommer dynamisk obalans att vara svår att eliminera (se figur 4), eftersom det i detta fall är svårt att installera korrigerande vikter som skapar det nödvändiga kompensationsmomentet.
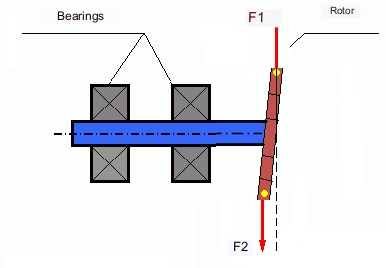
Krafterna F1 och F2 ligger inte på samma linje och kompenserar inte varandra.
Eftersom armen som ska skapa vridmoment är liten på grund av den smala rotorn, kan stora korrektionsvikter krävas. Detta resulterar dock också i en "inducerad obalans" på grund av deformation av den smala rotorn av centrifugalkrafter från korrektionsvikterna. (Se till exempel "Metodologiska instruktioner för balansering av styva rotorer (enligt ISO 22061-76)". Avsnitt 10. ROTORSTÖDSYSTEM.)
Detta är märkbart för smala fläkthjul, där, förutom kraftobalans, aerodynamisk obalans också är aktiv. Och det bör förstås att aerodynamisk obalans, eller snarare aerodynamisk kraft, är direkt proportionell mot rotorns vinkelhastighet, och för dess kompensation används centrifugalkraften hos korrigeringsmassan, som är proportionell mot kvadraten på vinkelhastigheten. Därför kan balanseringseffekten endast ske vid en specifik balanseringsfrekvens. Vid andra rotationsfrekvenser uppstår ett ytterligare fel.
Detsamma gäller för de elektromagnetiska krafterna i en elmotor, som också är proportionella mot vinkelhastigheten. Det är alltså inte möjligt att eliminera alla orsaker till vibrationer i en maskin genom balansering.
Vibrationer av mekanismer
Vibration är mekanismens reaktion på effekterna av en cyklisk excitatorisk kraft. Denna kraft kan vara av olika karaktär.
Centrifugalkraften som uppstår från den obalanserade rotorn är en okompenserad kraft som verkar på den "tunga punkten". Det är denna kraft och den vibration som orsakas av den som kan elimineras genom att balansera rotorn.
Interaktionskrafter av "geometrisk" natur som uppstår på grund av tillverknings- och monteringsfel i de sammankopplade delarna. Dessa krafter kan till exempel uppstå till följd av att axelhalsarna inte är runda, fel i kuggprofilerna i kugghjulen, vågighet i lagerbanorna, feljustering av sammankopplade axlar etc. Vid icke-cirkuläritet hos lagertapparna kommer axelaxeln att förskjutas beroende på axelns rotationsvinkel. Även om denna vibration också uppstår vid rotorhastighet är det nästan omöjligt att eliminera den genom balansering.
Aerodynamiska krafter som uppstår vid rotation av fläkthjul och andra skovelmekanismer. Hydrodynamiska krafter som uppstår vid rotation av impellrar i hydraulpumpar, turbiner etc.
Elektromagnetiska krafter som uppstår vid drift av elektriska maskiner, t.ex. asymmetriska rotorlindningar, kortslutna lindningar etc.
Vibrationens storlek (t.ex. dess amplitud Av) beror inte bara på den excitatoriska kraften Fv som verkar på mekanismen med cirkulär frekvens ω, utan också på mekanismens styvhet k, dess massa m samt dämpningskoefficienten C.
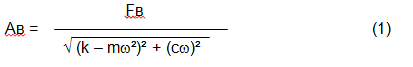
Olika typer av sensorer kan användas för att mäta vibrationer och balansmekanismer, t.ex:
- Absoluta vibrationsgivare konstruerade för att mäta vibrationsacceleration (accelerometrar) och vibrationshastighet (hastighetssensorer);
- relativa vibrationssensorer - virvelströms- eller kapacitiva, utformade för att mäta vibrationsförskjutning;
- I vissa fall (när mekanismens konstruktion tillåter det) kan kraftsensorer också användas för att bedöma dess vibrationsbelastning; i synnerhet används de i stor utsträckning för att mäta vibrationsbelastningen på hårdlagrade balanseringsmaskinstöd.
Vibrationer är alltså en maskins reaktion på yttre krafter. Vibrationens storlek beror inte bara på storleken på den kraft som verkar på mekanismen, utan också på styvheten i mekanismkonstruktionen. En och samma kraft kan leda till olika vibrationer. I en maskin med hårda lager kan lagren utsättas för betydande dynamiska belastningar, även om vibrationerna är små. Därför används kraftgivare (vibrationsaccelerometrar) i stället för vibrationsgivare vid balansering av maskiner med hårda lager.
Vibrationssensorer används på mekanismer med relativt böjliga stöd, när obalanserade centrifugalkrafter leder till en märkbar deformation av stöden och vibrationer. Kraftsensorer används för styva stöd, när även betydande krafter på grund av obalans inte leder till betydande vibrationer.
Resonans är en faktor som förhindrar balansering
Tidigare nämnde vi att rotorer delas in i styva och flexibla. Rotorns styvhet eller flexibilitet bör inte förväxlas med styvheten eller rörligheten hos de stöd (fundament) som rotorn är installerad på. En rotor anses vara styv när dess deformation (böjning) under inverkan av centrifugalkrafter kan försummas. Deformationen av en flexibel rotor är relativt stor och kan inte försummas.
I den här artikeln behandlar vi endast balansering av stela rotorer. En stel (icke-deformerbar) rotor kan i sin tur vara monterad på stela eller rörliga (böjliga) stöd. Det är uppenbart att stödets styvhet/upphängningsförmåga också är relativ, beroende på rotorvarvtalet och storleken på de resulterande centrifugalkrafterna. En villkorlig gräns är frekvensen för naturliga vibrationer hos rotorstöden.
För mekaniska system bestäms formen och frekvensen hos naturliga vibrationer av massan och elasticiteten hos elementen i det mekaniska systemet. Det vill säga, frekvensen för naturliga vibrationer är en intern egenskap hos det mekaniska systemet och beror inte på yttre krafter. När de avböjs från jämviktstillståndet tenderar stöd på grund av elasticitet att återgå till jämviktsläget. Men på grund av trögheten hos den massiva rotorn har denna process karaktären av dämpade svängningar. Dessa vibrationer är de naturliga vibrationerna i rotor-stödsystemet. Deras frekvens beror på förhållandet mellan rotorns massa och stödens elasticitet.
När rotorn börjar rotera och rotationsfrekvensen närmar sig frekvensen för naturliga vibrationer, ökar vibrationsamplituden kraftigt, vilket kan leda till att strukturen förstörs.
Fenomenet med mekanisk resonans uppstår. I resonansområdet kan en förändring av rotationshastigheten med 100 varv/min leda till en tiofaldig ökning av vibrationerna. Samtidigt (i resonansområdet) ändras vibrationsfasen 180°.
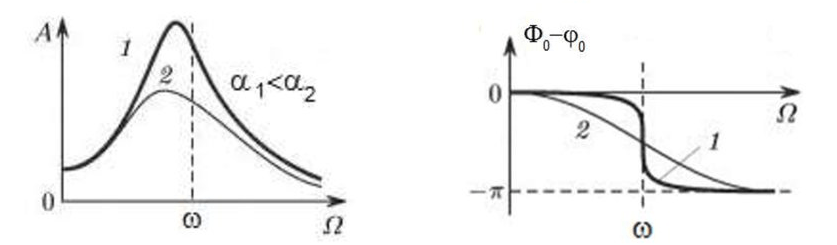
Om konstruktionen av mekanismen är misslyckad och rotorns arbetsfrekvens ligger nära frekvensen för naturliga vibrationer, blir mekanismens funktion omöjlig på grund av den otillåtet höga vibrationen. Detta är inte möjligt på vanligt sätt, eftersom även en liten hastighetsförändring kommer att orsaka en drastisk förändring av vibrationsparametrarna. För balansering inom resonansområdet används speciella metoder som inte beaktas i denna artikel.
Det är möjligt att bestämma frekvensen för mekanismens naturliga vibrationer vid utrullning (när rotorn stängs av) eller genom chockmetoden med efterföljande spektralanalys av systemets respons på chocken.
För mekanismer vars arbetsrotationsfrekvens ligger över resonansfrekvensen, dvs. som arbetar i resonansläge, anses stöden vara i rörelse och för mätning används vibrationsgivare, huvudsakligen vibroacelerometrar, som mäter accelerationen hos strukturella element. För mekanismer som arbetar i preresonant läge anses stöden vara stela. I detta fall används kraftsensorer.
Linjära och icke-linjära modeller av ett mekaniskt system. Icke-linjäritet är en faktor som förhindrar balansering
Vid balansering av stela rotorer används matematiska modeller som kallas linjära modeller för balanseringsberäkningar. En linjär modell innebär att i en sådan modell är den ena storheten proportionell (linjär) mot den andra. Om t.ex. den okompenserade massan på rotorn fördubblas, kommer vibrationsvärdet också att fördubblas. För stela rotorer kan en linjär modell användas, eftersom de inte deformeras.
För flexibla rotorer kan den linjära modellen inte längre användas. För en flexibel rotor, om massan av den tunga punkten ökar under rotation, kommer ytterligare deformation att uppstå, och förutom massan kommer radien för platsen för den tunga punkten också att öka. För en flexibel rotor kommer därför vibrationen att öka mer än två gånger, och de vanliga beräkningsmetoderna fungerar inte.
Även förändringen av stödens elasticitet vid deras stora deformationer, till exempel när vid små deformationer av stöd vissa strukturella element fungerar och vid stora är andra strukturella element involverade. Det är därför du inte kan balansera mekanismer som inte är fixerade på en grund, utan till exempel helt enkelt placerade på golvet. Vid kraftiga vibrationer kan obalansens kraft dra upp mekanismen från golvet och därmed väsentligt förändra systemets styvhetsegenskaper. Motorfötterna måste vara ordentligt fastsatta, bultfästena måste vara åtdragna, brickornas tjocklek måste ge tillräcklig monteringsstyvhet osv. Om lagren är trasiga kan det uppstå betydande axelförskjutningar och stötar, vilket också leder till dålig linjäritet och oförmåga att utföra en kvalitetsbalansering.
Balanseringsanordningar och balanseringsmaskiner
Som nämnts ovan är balansering processen att justera den huvudsakliga centrala tröghetsaxeln med rotorns rotationsaxel.
Denna process kan utföras med två metoder.
Den första metoden innebär att rotortapparna bearbetas på ett sådant sätt att axeln som går genom tapparnas centrum korsar rotorns centrala tröghetsaxel. En sådan teknik används sällan i praktiken och kommer inte att diskuteras i detalj i denna artikel.
Den andra (vanligaste) metoden innebär att man flyttar, installerar eller tar bort korrigeringsvikter på rotorn, som placeras så att rotorns tröghetsaxel ligger så nära dess rotationsaxel som möjligt.
Att flytta, lägga till eller ta bort korrektionsvikter under balanseringen kan göras med olika tekniska metoder, t.ex. borrning, fräsning, ytbearbetning, svetsning, skruvning eller lossning, bränning med laser eller elektronstråle, elektrolys, elektromagnetisk ytbearbetning etc.
Balanseringsprocessen kan åstadkommas på två sätt:
- Balansering av monterade rotorer (i sina egna lager) med hjälp av balanseringsmaskiner;
- Balansering av rotorer på balanseringsmaskiner. För balansering av rotorer i sina egna lager används vanligtvis specialiserade balanseringsanordningar (kit), som gör det möjligt att mäta vibrationen hos den balanserade rotorn vid dess rotationsfrekvens i vektorform, dvs. att mäta både amplitud och fas av vibrationen. För närvarande tillverkas ovanstående enheter på grundval av mikroprocessorteknik och (förutom vibrationsmätning och analys) tillhandahåller automatisk beräkning av parametrar för korrigeringsvikter, som bör installeras på rotorn för att kompensera dess obalans.
Dessa enheter inkluderar:
- en mät- och beräkningsenhet baserad på en dator eller industriell styrenhet;
- Två (eller fler) vibrationsgivare;
- En fasvinkelgivare;
- tillbehör för montering av sensorerna på plats;
- specialiserad programvara som är utformad för att utföra en fullständig cykel av mätning av rotorns vibrationsparametrar i ett, två eller flera korrigeringsplan.
Två typer av balanseringsmaskiner är för närvarande de vanligaste:
- Mjukbärande maskiner (med mjuka stöd);
- Maskiner med hårda lager (med styva stöd).
Maskiner med mjuka lager har relativt böjliga stöd, till exempel baserade på plana fjädrar. Frekvensen för naturliga vibrationer hos dessa stöd är vanligtvis 2-3 gånger lägre än rotationsfrekvensen för den balanserande rotorn som är monterad på dem. Vibrationssensorer (accelerometrar, vibrationshastighetssensorer etc.) används vanligtvis vid mätning av vibrationer i maskinens förresonanta stöd.
Maskiner för balansering före resonans använder relativt styva stöd, vars naturliga vibrationsfrekvenser bör vara 2-3 gånger högre än rotationsfrekvensen för den rotor som balanseras. Kraftgivare används vanligtvis för att mäta vibrationsbelastningen på preresonansmaskinens stöd.
Fördelen med förresonansbalanseringsmaskiner är att balansering på dem kan utföras vid relativt låga rotorhastigheter (upp till 400-500 rpm), vilket avsevärt förenklar maskinens och dess fundaments design, samt ökar produktiviteten och säkerheten vid balansering.
Balansering av styva rotorer
Viktigt!
- Balansering eliminerar endast vibrationer som orsakas av asymmetrisk fördelning av rotormassan i förhållande till rotationsaxeln. Andra typer av vibrationer elimineras inte genom balansering!
- Tekniska mekanismer, vars konstruktion säkerställer frånvaron av resonanser vid den operativa rotationsfrekvensen, tillförlitligt fixerade på fundamentet, installerade i servicelager, är föremål för balansering.
- Defekta maskiner måste repareras före balansering. I annat fall är kvalitetsbalansering inte möjlig.
Balansering ersätter inte reparation!
Den viktigaste uppgiften vid balansering är att hitta massan och placeringen av kompensationsvikter som är föremål för balansering av centrifugalkrafter.
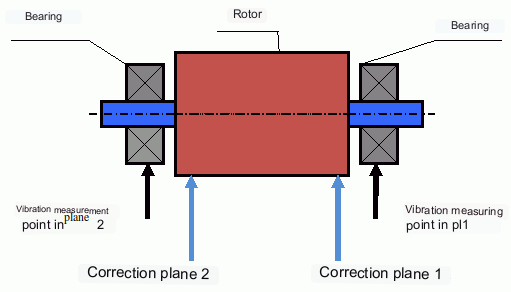
Som nämnts ovan är det för styva rotorer i allmänhet nödvändigt och tillräckligt att installera två kompensationsvikter. Detta kommer att eliminera både statisk och dynamisk obalans i rotorn. Det allmänna schemat för vibrationsmätning under balansering är som följer.
Vibrationsgivare är installerade på lagerstöden vid punkterna 1 och 2. En varvtalsmarkering fästs på rotorn, vanligtvis med reflekterande tejp. Varvtalsmarkeringen används av lasertakometern för att bestämma rotorns varvtal och vibrationssignalens fas.
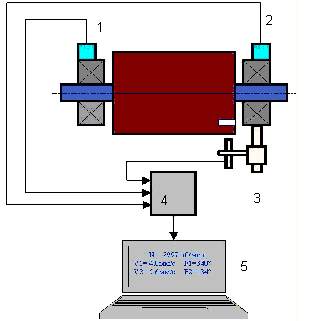
Hur dynamisk balansering utförs (trestegsmetoden)
I de flesta fall utförs dynamisk balansering med metoden för tre starter. Metoden bygger på att provvikter med känd vikt placeras på rotorn i serie i plan 1 och 2 och vikterna och placeringen av balanseringsvikterna beräknas utifrån resultaten av förändringar i vibrationsparametrarna.
Platsen för installation av vikter kallas korrektionsplanet. Vanligtvis väljs korrektionsplanen i området för de lagerstöd på vilka rotorn är installerad.
Vid den första uppstarten mäts den initiala vibrationen. Därefter placeras en testvikt med känd vikt på rotorn närmare ett av lagren. En andra uppstart utförs och vibrationsparametrarna mäts, vilka bör förändras på grund av provviktens installation. Därefter avlägsnas testvikten i det första planet och installeras i det andra planet. En tredje provkörning utförs och vibrationsparametrarna mäts. Testvikten avlägsnas och programvaran beräknar automatiskt massorna och installationsvinklarna för balansvikterna.
Syftet med att installera testvikter är att fastställa hur systemet reagerar på förändringar i obalansen. Testvikternas vikter och placering är kända, så programvaran kan beräkna så kallade påverkanskoefficienter, som visar hur införandet av en känd obalans påverkar vibrationsparametrarna. Påverkanskoefficienterna är egenskaper hos det mekaniska systemet i sig och beror på stödets styvhet och massan (trögheten) hos rotor-stödsystemet.
För samma typ av mekanismer med samma konstruktion kommer påverkanskoefficienterna att ligga nära varandra. Det är möjligt att spara dem i datorns minne och använda dem för balansering av samma typ av mekanismer utan testkörningar, vilket avsevärt ökar produktiviteten vid balansering. Observera att testvikternas massa bör väljas så att vibrationsparametrarna ändras märkbart när testvikterna installeras. I annat fall ökar felet vid beräkning av påverkanskoefficienter och kvaliteten på balanseringen försämras.
Som framgår av fig. 1 verkar centrifugalkraften i radiell riktning, dvs. vinkelrätt mot rotoraxeln. Därför måste vibrationsgivarna installeras så att deras känslighetsaxel också pekar i radiell riktning. Vanligtvis är fundamentets styvhet i horisontell riktning mindre, så vibrationerna i horisontell riktning är högre. För att öka känsligheten bör sensorerna därför installeras så att deras känslighetsaxel också riktas horisontellt. Även om det inte finns någon grundläggande skillnad. Förutom vibrationer i radiell riktning måste även vibrationer i axiell riktning, längs rotorns rotationsaxel, övervakas. Denna vibration orsakas vanligtvis inte av obalans, utan av andra orsaker, främst relaterade till felinriktning och felinriktning av axlarna som är anslutna via kopplingen.
Denna vibration kan inte elimineras genom balansering, i vilket fall uppriktning krävs. I praktiken har sådana maskiner vanligtvis både rotorobalans och axelfeljustering, vilket gör uppgiften att eliminera vibrationer mycket svårare. I sådana fall är det nödvändigt att centrera maskinen först och sedan balansera den. (Även om vibrationer även uppstår i axiell riktning vid stark momentobalans på grund av "vridning" av fundamentstrukturen.)
Relaterade artiklar (exempel på balanseringsställ)
- Balansställning med mjukt stöd
- Balansering av rotorer i elmotorer
- Enkla men effektiva balanseringsställningar
Kriterier för bedömning av kvaliteten på balanseringsmekanismer
Balanseringskvaliteten hos rotorer (mekanismer) kan utvärderas på två sätt. Den första metoden innebär att man jämför mängden kvarvarande obalans som fastställts under balanseringsprocessen med toleransen för kvarvarande obalans. Dessa toleranser för de olika rotorklasserna är specificerade i ISO 1940-1-2007. Del 1. Definition av tillåten obalans.
Överensstämmelse med de angivna toleranserna kan emellertid inte helt garantera mekanismens driftsäkerhet, som är förknippad med uppnåendet av den lägsta nivån av dess vibrationer. Detta förklaras av det faktum att storleken på mekanismens vibrationer inte bara bestäms av storleken på den kraft som är förknippad med den kvarvarande obalansen i dess rotor, utan också beror på flera andra parametrar, inklusive: styvheten k hos mekanismens strukturella element, dess massa m, dämpningsfaktorn samt rotationsfrekvensen. För att uppskatta mekanismens dynamiska egenskaper (inklusive kvaliteten på dess balans) rekommenderas därför i ett antal fall att uppskatta mekanismens nivå av kvarvarande vibrationer, vilket regleras av ett antal standarder.
Den vanligaste standarden, som reglerar de tillåtna vibrationsnivåerna för mekanismer, är ISO 10816-3-2002. Med hjälp av den är det möjligt att ställa in toleranser för alla typer av maskiner, med hänsyn till kraften i deras elektriska drivning.
Förutom denna universella standard finns det ett antal specialiserade standarder som utvecklats för specifika typer av maskiner. Till exempel 31350-2007 , ISO 7919-1-2002, etc.
Standarder och referenser
- ISO 1940-1:2007. Vibration. Krav för balanseringskvalitet hos stela rotorer. Del 1. Bestämning av tillåten obalans.
- ISO 10816-3:2009. Mekanisk vibration – Utvärdering av maskinvibrationer genom mätningar på icke-roterande delar – Del 3: Industrimaskiner med nominell effekt över 15 kW och nominella varvtal mellan 120 r/min och 15 000 r/min vid mätning på plats.
- ISO 14694:2003. Industrifläktar — Specifikationer för balanskvalitet och vibrationsnivåer.
- ISO 7919-1:2002. Vibrationer hos maskiner utan fram- och återgående rörelse – Mätningar på roterande axlar och utvärderingskriterier – Allmänna riktlinjer.
VANLIGA FRÅGOR
Tar balansering bort alla vibrationer?
Nej. Balansering tar bort vibrationer orsakade av den asymmetriska fördelningen av rotormassan i förhållande till dess rotationsaxel. Vibrationer från feljustering, lagerdefekter, aerodynamiska/hydrodynamiska krafter, elektromagnetiska krafter och andra orsaker kräver separat diagnostik och korrigerande åtgärder.
Varför kan balansering misslyckas nära resonans?
Nära resonans kan små hastighetsförändringar orsaka stora förändringar i vibrationsamplituden och en fasförskjutning på 180°. Under sådana förhållanden blir mätresultaten instabila, och konventionella balanseringsprocedurer kanske inte konvergerar utan speciella metoder.
När behöver man balansering i ett plan kontra två plan?
För en stel rotor är två vikter separerade längs rotorns längd i allmänhet nödvändiga och tillräckliga för att eliminera kombinerad statisk och dynamisk obalans. Smala rotorer uppvisar ofta mestadels statisk obalans, men deformation och geometri kan introducera en dynamisk komponent som kan kräva korrigering i två plan.
Vad bör göras innan balansering?
Säkerställ att maskinen är funktionsduglig: tillförlitlig montering på fundamentet, felfria lager, ingen allvarlig glapp och inga uppenbara källor till icke-linjäritet. Balansering ersätter inte reparation.
Viktiga slutsatser
- Balansering korrigerar massrelaterad (centrifugal) excitation; den löser inte feljustering, lagerskador eller elektromagnetiska/aerodynamiska källor.
- Resonans och icke-linjäritet kan göra konventionell balansering ineffektiv eller osäker.
- För stela rotorer är tvåplansbalansering den generella lösningen för kombinerad statisk + dynamisk obalans.






