Linear and Nonlinear Vibrations, Their Features, and Balancing Methods
Rotating mechanisms surround us everywhere – from miniature fans in computers to giant turbines at power plants. Their reliable and efficient operation directly depends on balancing – the process of eliminating mass imbalances that lead to unwanted vibrations. Vibrations, in turn, not only reduce the performance and lifespan of equipment but can also cause serious accidents and injuries. Therefore, balancing is a crucial procedure in the production, operation, and maintenance of rotating equipment.
Successful balancing requires understanding how an object reacts to the addition or removal of mass. In this context, the concepts of linear and nonlinear objects play a key role. Understanding whether an object is linear or nonlinear allows the selection of the correct balancing strategy and helps achieve the desired result.
Linear objects hold a special place in this field due to their predictability and stability. They allow for the use of simple and reliable diagnostic and balancing methods, making their study an important step in vibration diagnostics.
What Are Linear Objects?
A linear object is a system where vibration is directly proportional to the magnitude of imbalance.
A linear object, in the context of balancing, is an idealized model characterized by a direct proportional relationship between the magnitude of the imbalance (unbalanced mass) and the vibration amplitude. This means that if the imbalance is doubled, the vibration amplitude will also double, provided the rotor’s rotational speed remains constant. Conversely, reducing the imbalance will proportionally decrease the vibrations.
Unlike nonlinear systems, where the behavior of an object may vary depending on many factors, linear objects allow for a high level of precision with minimal effort.
Additionally, they serve as the foundation for training and practice for balancers. Understanding the principles of linear objects helps develop skills that can later be applied to more complex systems.
Graphical Representation of Linearity
Imagine a graph where the horizontal axis represents the magnitude of the unbalanced mass (imbalance), and the vertical axis represents the vibration amplitude. For a linear object, this graph will be a straight line passing through the origin (the point where both the imbalance magnitude and the vibration amplitude are zero). The slope of this line characterizes the object’s sensitivity to imbalance: the steeper the slope, the greater the vibrations for the same imbalance.
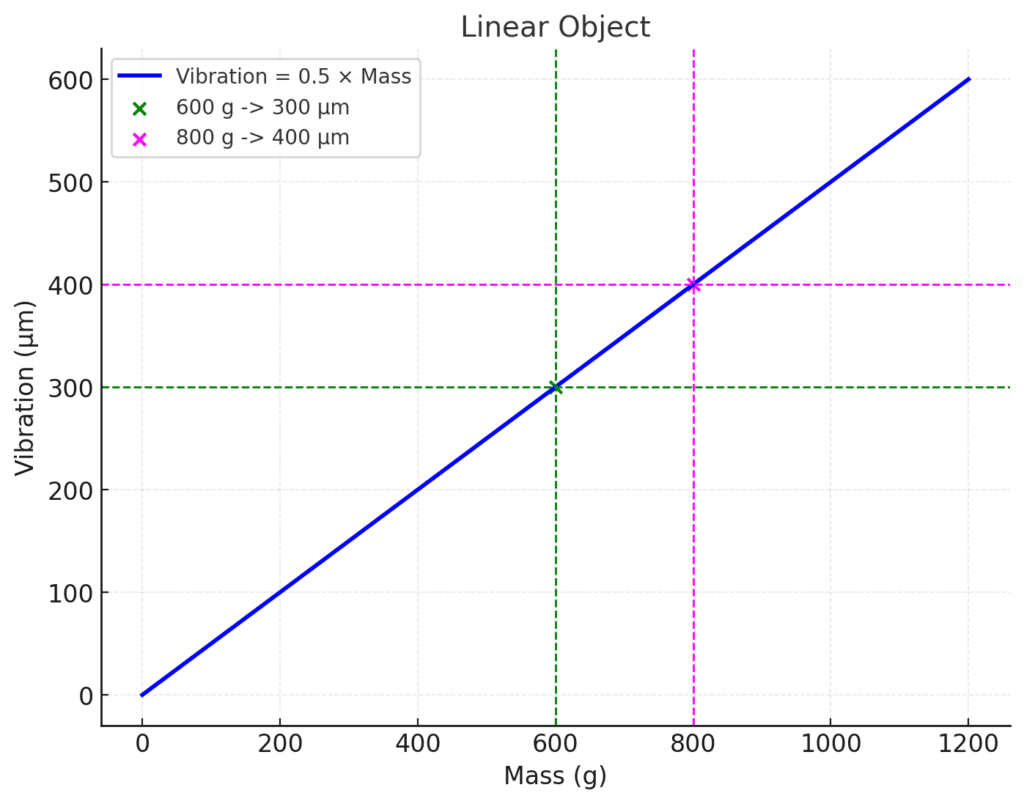
Graph 1: The Relationship Between Vibration Amplitude (µm) and Unbalanced Mass (g)
Graph 1 illustrates the relationship between the vibration amplitude (µm) of a linear balancing object and the unbalanced mass (g) of the rotor. The proportionality coefficient is 0.5 µm/g. Simply dividing 300 by 600 gives 0.5 µm/g. For an unbalanced mass of 800 g (UM=800 g), the vibration will be 800 g * 0.5 µm/g = 400 µm. Note that this applies at a constant rotor speed. At a different rotational speed, the coefficient will be different.
This proportionality coefficient is called the influence coefficient (sensitivity coefficient) and has a dimension of µm/g or, in cases involving imbalance, µm/(g*mm), where (g*mm) is the unit of imbalance. Knowing the influence coefficient (IC), it is also possible to solve the inverse problem, namely, determining the unbalanced mass (UM) based on the vibration magnitude. To do this, divide the vibration amplitude by the IC.
For example, if the measured vibration is 300 µm and the known coefficient is IC=0.5 µm/g, divide 300 by 0.5 to get 600 g (UM=600 g).
Influence Coefficient (IC): Key Parameter of Linear Objects
A critical characteristic of a linear object is the influence coefficient (IC). It is numerically equal to the tangent of the slope angle of the line on the graph of vibration versus imbalance and indicates how much the vibration amplitude (in microns, µm) changes when a unit of mass (in grams, g) is added in a specific correction plane at a specific rotor speed. In other words, IC is a measure of the object’s sensitivity to imbalance. Its unit of measurement is µm/g, or, when imbalance is expressed as the product of mass and radius, µm/(g*mm).
IC is essentially the “passport” characteristic of a linear object, enabling predictions of its behavior when mass is added or removed. Knowing the IC allows solving both the direct problem – determining vibration magnitude for a given imbalance – and the inverse problem – calculating imbalance magnitude from measured vibration.
Direct Problem:
• Vibration Amplitude (µm) = IC (µm/g) * Unbalanced Mass (g)
Inverse Problem:
• Unbalanced Mass (g) = Vibration Amplitude (µm) / IC (µm/g)
Vibration Phase in Linear Objects
In addition to amplitude, vibration is also characterized by its phase, which indicates the rotor’s position at the moment of maximum deviation from its equilibrium position. For a linear object, the vibration phase is also predictable. It is the sum of two angles:
- The angle that determines the position of the rotor’s overall unbalanced mass. This angle indicates the direction in which the primary imbalance is concentrated.
- The argument of the influence coefficient. This is a constant angle that characterizes the object’s dynamic properties and does not depend on the magnitude or angle of the unbalanced mass installation.
Thus, by knowing the IC argument and measuring the vibration phase, it is possible to determine the angle of the unbalanced mass installation. This allows not only the calculation of the corrective mass magnitude but also its precise placement on the rotor to achieve optimal balance.
Balancing Linear Objects
It is important to note that for a linear object, the influence coefficient (IC) determined in this way does not depend on the magnitude or angle of the trial mass installation, nor on the initial vibration. This is a key characteristic of linearity. If the IC remains unchanged when the trial mass parameters or initial vibration are altered, it can be confidently asserted that the object behaves linearly within the considered range of imbalances.
Steps for Balancing a Linear Object
- Measuring Initial Vibration:
The first step is to measure the vibration in its initial state. The amplitude and vibration angle, which indicate the imbalance direction, are determined. - Installing a Trial Mass:
A mass of known weight is installed on the rotor. This helps to understand how the object reacts to additional loads and allows the vibration parameters to be calculated. - Re-measuring Vibration:
After installing the trial mass, new vibration parameters are measured. By comparing them with the initial values, it is possible to determine how the mass affects the system. - Calculating the Corrective Mass:
Based on the measurement data, the mass and installation angle of the corrective weight are determined. This weight is placed on the rotor to eliminate the imbalance. - Final Verification:
After installing the corrective weight, the vibration should be significantly reduced. If the residual vibration still exceeds the acceptable level, the procedure can be repeated.
Linear objects serve as ideal models for studying and practically applying balancing methods. Their properties allow engineers and diagnosticians to focus on developing basic skills and understanding the fundamental principles of working with rotor systems. Although their application in real practice is limited, the study of linear objects remains an important step in advancing vibration diagnostics and balancing.
These objects form the basis for developing methods and tools that are later adapted for working with more complex systems, including nonlinear objects. Ultimately, understanding the operation of linear objects helps ensure stable and reliable equipment performance, minimize vibrations, and extend its service life.
Nonlinear Objects: When Theory Diverges from Practice
What Is a Nonlinear Object?
A nonlinear object is a system where the vibration amplitude is not proportional to the magnitude of imbalance. Unlike linear objects, where the relationship between vibration and imbalance mass is represented by a straight line, in nonlinear systems this relationship can follow complex trajectories.
In the real world, not all objects behave linearly. Nonlinear objects exhibit a relationship between imbalance and vibration that is not directly proportional. This means the influence coefficient is not constant and may vary depending on several factors, such as:
- Magnitude of Imbalance: Increasing the imbalance can change the stiffness of the rotor’s supports, leading to nonlinear changes in vibration.
- Rotational Speed: Different resonance phenomena may be excited at varying rotational speeds, also resulting in nonlinear behavior.
- Presence of Clearances and Gaps: Clearances and gaps in bearings and other connections can cause abrupt changes in vibration under certain conditions.
- Temperature: Temperature changes can affect material properties and, consequently, the vibration characteristics of the object.
- External Loads: External loads acting on the rotor can alter its dynamic characteristics and lead to nonlinear behavior.
Why Are Nonlinear Objects Challenging?
Nonlinearity introduces many variables into the balancing process. Successful work with nonlinear objects requires more measurements and more complex analysis. For instance, standard methods applicable to linear objects do not always yield accurate results for nonlinear systems. This necessitates a deeper understanding of the physics of the process and the use of specialized diagnostic methods.
Signs of Nonlinearity
A nonlinear object can be identified by the following signs:
- Non-proportional vibration changes: As the imbalance increases, vibration may grow faster or slower than expected for a linear object.
- Phase shift in vibration: The vibration phase may change unpredictably with variations in imbalance or rotational speed.
- Presence of harmonics and subharmonics: The vibration spectrum may exhibit higher harmonics (multiples of the rotational frequency) and subharmonics (fractions of the rotational frequency), indicating nonlinear effects.
- Hysteresis: The vibration amplitude may depend not only on the current value of imbalance but also on its history. For example, when imbalance is increased and then decreased back to its initial value, the vibration amplitude may not return to its original level.
Nonlinearity introduces many variables into the balancing process. More measurements and complex analysis are required for successful operation. For example, standard methods applicable to linear objects do not always yield accurate results for nonlinear systems. This necessitates a deeper understanding of the process physics and the use of specialized diagnostic methods.
Graphical Representation of Nonlinearity
On a graph of vibration versus imbalance, nonlinearity is evident in deviations from a straight line. The graph may feature bends, curvature, hysteresis loops, and other characteristics that indicate a complex relationship between imbalance and vibration.
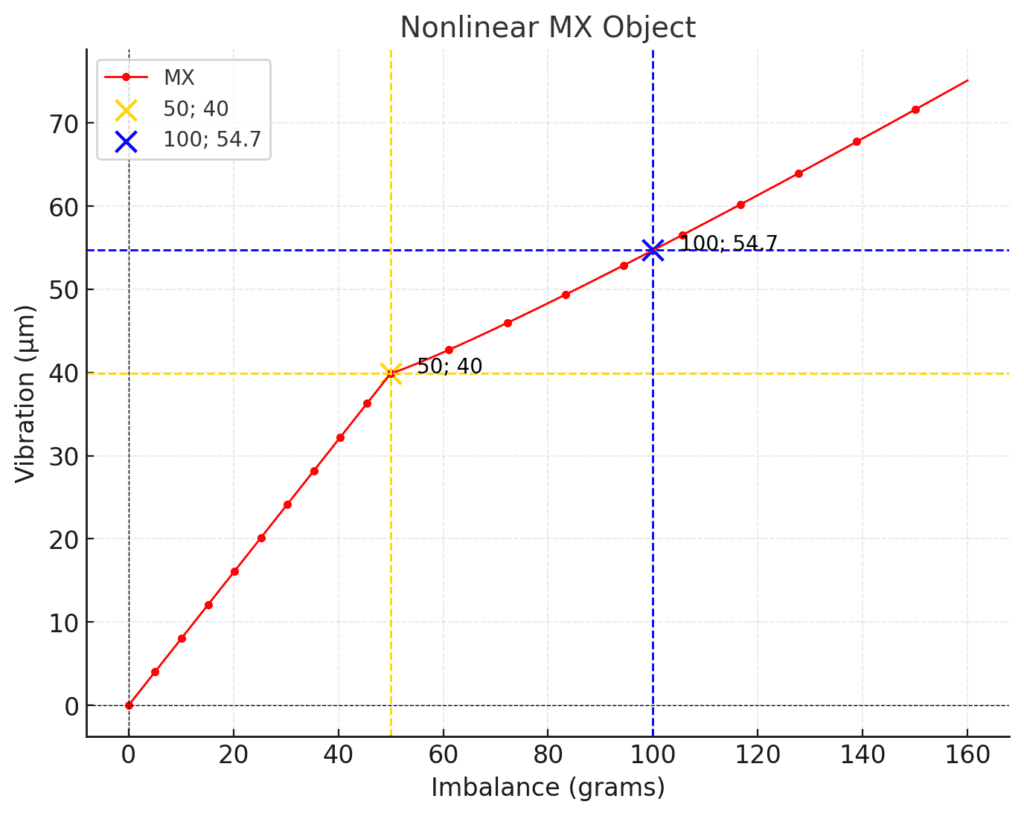
Graph 2. Nonlinear Object
50g; 40μm (yellow),
100g; 54.7μm (blue).
This object exhibits two segments, two straight lines. For imbalances less than 50 grams, the graph reflects the properties of a linear object, maintaining proportionality between the imbalance in grams and the vibration amplitude in microns. For imbalances greater than 50 grams, the growth of the vibration amplitude slows down.
Examples of Nonlinear Objects
Examples of nonlinear objects in the context of balancing include:
- Rotors with cracks: Cracks in the rotor can lead to nonlinear changes in stiffness and, as a result, a nonlinear relationship between vibration and imbalance.
- Rotors with bearing clearances: Clearances in bearings can cause abrupt changes in vibration under certain conditions.
- Rotors with nonlinear elastic elements: Some elastic elements, such as rubber dampers, may exhibit nonlinear characteristics, affecting the rotor’s dynamics.
Types of Nonlinearity
1. Soft-Stiff Nonlinearity
In such systems, two segments are observed: soft and stiff. In the soft segment, the behavior resembles linearity, where the vibration amplitude increases proportionally to the imbalance mass. However, after a certain threshold (breakpoint), the system transitions to a stiff mode, where the amplitude growth slows down.
2. Elastic Nonlinearity
Changes in the stiffness of supports or contacts within the system make the vibration-imbalance relationship complex. For instance, vibration may suddenly increase or decrease when crossing specific load thresholds.
3. Friction-Induced Nonlinearity
In systems with significant friction (e.g., in bearings), the vibration amplitude may be unpredictable. Friction can reduce vibration in one speed range and amplify it in another.
Balancing Nonlinear Objects: A Complex Task with Unconventional Solutions
Balancing nonlinear objects is a challenging task that requires specialized methods and approaches. The standard trial mass method, developed for linear objects, may yield erroneous results or be entirely inapplicable.
Balancing Methods for Nonlinear Objects
- Step-by-step balancing:
This method involves gradually reducing imbalance by installing corrective weights at each stage. After each stage, vibration measurements are taken, and a new corrective weight is determined based on the object’s current state. This approach accounts for changes in the influence coefficient during the balancing process. - Balancing at multiple speeds:
This method addresses the effects of resonance phenomena at different rotational speeds. Balancing is performed at several speeds near resonance, enabling more uniform vibration reduction across the entire operating speed range. - Using mathematical models:
For complex nonlinear objects, mathematical models describing rotor dynamics while accounting for nonlinear effects can be employed. These models help predict object behavior under various conditions and determine optimal balancing parameters.
The experience and intuition of a specialist play a crucial role in balancing nonlinear objects. An experienced balancer can recognize signs of nonlinearity, select an appropriate method, and adapt it to the specific situation. Analyzing vibration spectra, observing vibration changes as the object’s operating parameters vary, and considering the rotor’s design features all assist in making the right decisions and achieving the desired results.
How to Balance Nonlinear Objects Using a Tool Designed for Linear Objects
This is a good question. My personal method for balancing such objects starts with repairing the mechanism: replacing bearings, welding cracks, tightening bolts, checking anchors or vibration isolators, and verifying that the rotor does not rub against stationary structural elements.
Next, I identify resonance frequencies, as it is impossible to balance a rotor at speeds close to resonance. To do this, I use the impact method for resonance determination or a rotor coast-down graph.
Then, I determine the sensor’s position on the mechanism: vertical, horizontal, or at an angle.
After trial runs, the device indicates the angle and weight of the corrective loads. I halve the corrective load weight but use the angles suggested by the device for rotor placement. If the residual vibration after correction still exceeds the acceptable level, I perform another rotor run. Naturally, this takes more time, but the results are sometimes inspiring.
The Art and Science of Balancing Rotating Equipment
Balancing rotating equipment is a complex process that combines elements of science and art. For linear objects, balancing involves relatively simple calculations and standard methods. However, working with nonlinear objects requires a deep understanding of rotor dynamics, the ability to analyze vibration signals, and the skill to choose the most effective balancing strategies.
Experience, intuition, and continuous skill improvement are what make a balancer a true master of their craft. After all, the quality of balancing not only determines the efficiency and reliability of equipment operation but also ensures the safety of people.







0 Comments