Rotorbalansering: statisk og dynamisk ubalanse, resonans og praktisk prosedyre
Denne veiledningen forklarer rotorbalansering for stive rotorer: hva “ubalanse” betyr, hvordan statisk og dynamisk ubalanse er forskjellig, hvorfor resonans og ikke-linearitet kan forhindre et kvalitetsresultat, og hvordan balansering vanligvis utføres i ett eller to korreksjonsplan.
Innhold
- Hva er en rotor, og hva korrigerer balansering?
- Typer rotorer og typer ubalanse
- Vibrasjon av mekanismer: hva balansering kan og ikke kan fjerne
- Resonans: en faktor som hindrer balansering
- Lineære vs. ikke-lineære modeller: når beregninger slutter å virke
- Balanseringsinnretninger og balanseringsmaskiner
- Balansering av stive rotorer (praktiske notater)
- Hvordan dynamisk balansering utføres (tre-run-metoden)
- Kriterier for vurdering av balanseringskvalitet
- Standarder og referanser
- VANLIGE SPØRSMÅL
Hva er en rotor, og hva korrigerer balansering?
Rotoren er et legeme som roterer rundt en akse og holdes fast av lagerflatene i støttene. Rotorens lagerflater overfører belastninger til støttene via rulle- eller glidelagre. Lagerflatene er overflatene på dreiehjulene eller overflatene som erstatter dem.
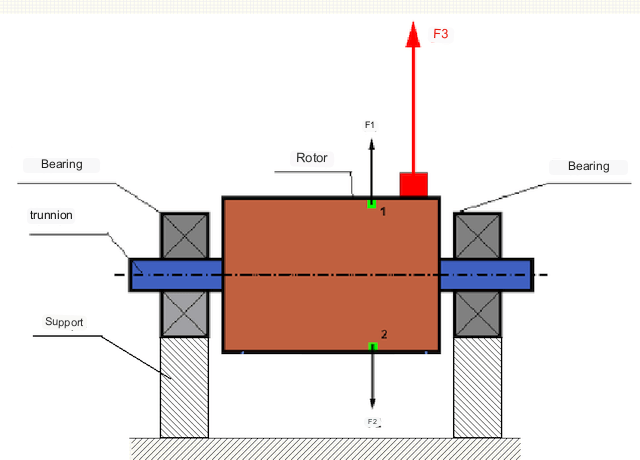
I en perfekt balansert rotor er massen fordelt symmetrisk rundt rotasjonsaksen, dvs. at ethvert element i rotoren kan matches med et annet element som er plassert symmetrisk rundt rotasjonsaksen. I en balansert rotor balanseres sentrifugalkraften som virker på ethvert rotorelement av sentrifugalkraften som virker på det symmetriske elementet. For eksempel virker sentrifugalkreftene F1 og F2, like store og motsatt i retning, på elementene 1 og 2 (markert grønt i figur 1). Dette gjelder for alle symmetriske rotorelementer, og dermed er den totale sentrifugalkraften som virker på rotoren 0 og rotoren er balansert.
Men hvis rotorens symmetri brytes (asymmetrisk element er markert med rød farge på figur 1), virker den ubalanserte sentrifugalkraften F3 på rotoren. Når den roterer, endrer denne kraften retning med rotorens rotasjon. Den dynamiske belastningen som følge av denne kraften overføres til lagrene, noe som resulterer i akselerert slitasje.
I tillegg oppstår det en syklisk deformasjon av støttene og fundamentet som rotoren er festet på, dvs. at det oppstår vibrasjoner under påvirkning av denne variable kraften. For å eliminere rotorubalansen og de medfølgende vibrasjonene må det installeres balanseringsmasser for å gjenopprette symmetrien i rotoren.
Rotorbalansering er en operasjon for å korrigere ubalanse ved å legge til balanseringsmasser.
Balansering går ut på å finne størrelsen og plasseringen (vinkelen) til en eller flere balanseringsmasser.
Typer rotorer og typer ubalanse
Med tanke på rotorens materiales styrke og størrelsen på sentrifugalkreftene som virker på den, kan rotorer deles inn i to typer - stive rotorer og fleksible rotorer.
Stive rotorer deformeres ubetydelig under påvirkning av sentrifugalkraften i arbeidsmodus, og denne deformasjonen kan derfor neglisjeres i beregningene.
Deformasjon av fleksible rotorer kan ikke lenger neglisjeres. Deformasjon av fleksible rotorer kompliserer løsningen av balanseringsproblemet og krever anvendelse av andre matematiske modeller i sammenligning med problemet med balansering av stive rotorer. Det bør bemerkes at den samme rotoren ved lave hastigheter kan oppføre seg som stiv, og ved høye hastigheter - som fleksibel. I det følgende vil vi kun vurdere balansering av stive rotorer.
Avhengig av fordelingen av ubalanserte masser langs rotorens lengde, kan man skille mellom to typer ubalanse - statisk og dynamisk (momentan). Følgelig refereres det til statisk og dynamisk rotorbalansering. Statisk rotorubalanse oppstår uten rotasjon av rotoren, dvs. i statikk, når rotoren reverseres av tyngdekraften med sitt "tunge punkt" nedover. Et eksempel på en rotor med statisk ubalanse er vist i figur 2.
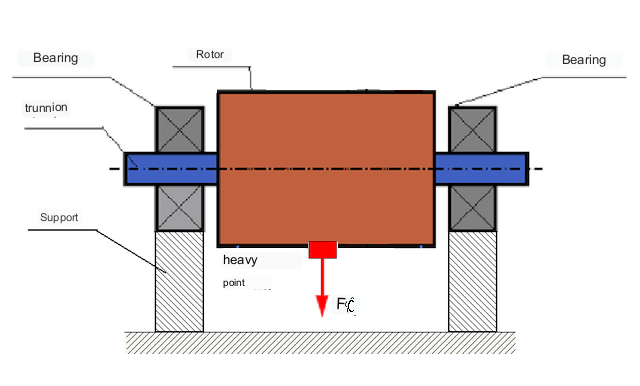
Dynamisk ubalanse oppstår bare når rotoren roterer.
Et eksempel på en rotor med dynamisk ubalanse er vist i figur 3.
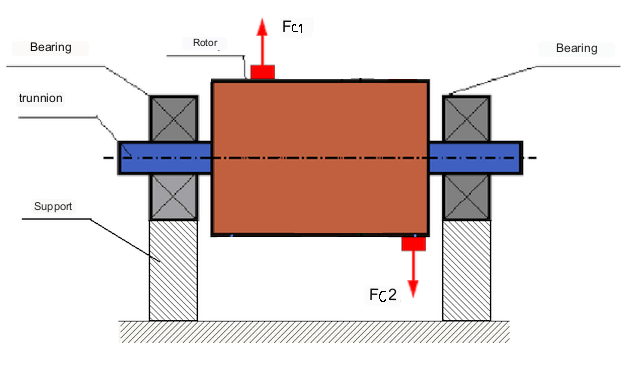
I dette tilfellet er de ubalanserte, like massene M1 og M2 i forskjellige plan - på forskjellige steder langs rotorens lengde. I statisk posisjon, dvs. når rotoren ikke roterer, virker bare tyngdekraften på rotoren, og massene balanserer hverandre. I dynamikk, når rotoren roterer, begynner sentrifugalkreftene Fc1 og Fc2 å virke på massene M1 og M2. Disse kreftene er like store og motsatt i retning. Men siden de påføres på forskjellige steder langs akselens lengde og ikke er på samme linje, kompenserer ikke disse kreftene hverandre. Kreftene Fc1 og Fc2 skaper et dreiemoment som påføres rotoren. Derfor kalles denne ubalansen også momentubalanse. Følgelig virker ukompenserte sentrifugalkrefter på lagerposisjonene, noe som kan overstige de beregnede verdiene i stor grad og redusere lagrenes levetid.
Siden denne typen ubalanse kun oppstår dynamisk under rotorens rotasjon, kalles den dynamisk ubalanse. Den kan ikke korrigeres under statiske forhold ved å balansere "på kniver" eller lignende metoder. For å eliminere dynamisk ubalanse må det installeres to kompenserende vekter, som produserer et moment som er likt i størrelse og motsatt i retning av momentet som oppstår fra massene M1 og M2. De kompenserende massene trenger ikke å settes motsatt og like i størrelse som massene M1 og M2. Hovedsaken er at de produserer et moment som fullt ut kompenserer for ubalansemomentet.
Generelt sett er massene M1 og M2 kanskje ikke like, så det vil være en kombinasjon av statisk og dynamisk ubalanse. Det er teoretisk bevist at for en stiv rotor er to vekter plassert langs rotorens lengde nødvendige og tilstrekkelige for å eliminere ubalansen. Disse vektene vil kompensere både dreiemomentet som følge av dynamisk ubalanse og sentrifugalkraften som følge av asymmetrien til massen i forhold til rotoraksen (statisk ubalanse). Typisk er dynamisk ubalanse karakteristisk for lange rotorer, som aksler, og statisk ubalanse er karakteristisk for smale rotorer. Men hvis den smale rotoren er skjev i forhold til aksen, eller deformert ("figur åtte"), vil dynamisk ubalanse være vanskelig å eliminere (se fig. 4), fordi det i dette tilfellet er vanskelig å installere korrigerende vekter som skaper det nødvendige kompenserende momentet.
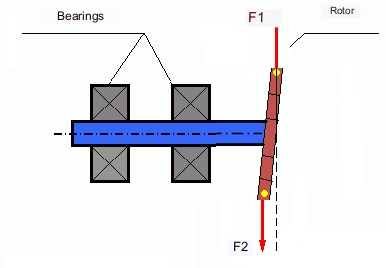
Kreftene F1 og F2 ligger ikke på samme linje og kompenserer ikke for hverandre.
Fordi armen som skal skape dreiemoment er liten på grunn av den smale rotoren, kan det være nødvendig med store korreksjonsvekter. Dette resulterer imidlertid også i en "indusert ubalanse" på grunn av deformasjon av den smale rotoren av sentrifugalkrefter fra korreksjonsvektene. (Se for eksempel "Metodologiske instruksjoner for balansering av stive rotorer (i henhold til ISO 22061-76)". Avsnitt 10. ROTORSTØTTESYSTEM.)
Dette merkes for smale løpehjul av vifter, der, i tillegg til kraftubalanse, også aerodynamisk ubalanse er aktiv. Og det skal forstås at aerodynamisk ubalanse, eller rettere sagt aerodynamisk kraft er direkte proporsjonal med rotorens vinkelhastighet, og for kompensasjon brukes sentrifugalkraften til korrigerende masse, som er proporsjonal med kvadratet av vinkelhastigheten. Derfor kan balanseringseffekten bare finne sted ved en spesifikk balanseringsfrekvens. Ved andre rotasjonsfrekvenser oppstår det en ekstra feil.
Det samme kan sies om de elektromagnetiske kreftene i en elektrisk motor, som også er proporsjonale med vinkelhastigheten. Det er altså ikke mulig å eliminere alle årsaker til vibrasjoner i en maskin ved hjelp av avbalansering.
Vibrasjon av mekanismer
Vibrasjon er mekanismens reaksjon på effekten av en syklisk eksitatorisk kraft. Denne kraften kan være av forskjellig art.
Sentrifugalkraften som følge av den ubalanserte rotoren er en ukompensert kraft som virker på det "tunge punktet". Det er denne kraften og vibrasjonen forårsaket av den som kan elimineres ved å balansere rotoren.
Vekselvirkningskrefter av "geometrisk" art som oppstår fra produksjons- og monteringsfeil i de sammenkoblede delene. Disse kreftene kan for eksempel oppstå som følge av at akselhalsene ikke er runde, feil i profilene til tennene i gir, bølgete lagerbaner, feiljustering av sammenkoblede aksler, osv. Ved ikke-sirkulære akseltapper vil akselaksen forskyves avhengig av akselens rotasjonsvinkel. Selv om denne vibrasjonen også oppstår ved rotorhastighet, er det nesten umulig å eliminere den ved å balansere.
Aerodynamiske krefter som oppstår ved rotasjon av viftehjul og andre skovlmekanismer. Hydrodynamiske krefter som skyldes rotasjon av løpehjul på hydrauliske pumper, turbiner osv.
Elektromagnetiske krefter som skyldes drift av elektriske maskiner, f.eks. asymmetriske rotorviklinger, kortsluttede viklinger osv.
Størrelsen på vibrasjonen (f.eks. amplituden Av) avhenger ikke bare av eksitasjonskraften Fv som virker på mekanismen med sirkulær frekvens ω, men også av mekanismens stivhet k, massen m og dempingskoeffisienten C.
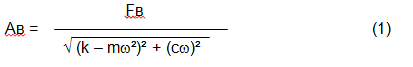
Ulike typer sensorer kan brukes til å måle vibrasjoner og balansemekanismer, blant annet:
- Absolutte vibrasjonssensorer designet for å måle vibrasjonsakselerasjon (akselerometre) og vibrasjonshastighet;
- sensorer for relativ vibrasjon - virvelstrøm eller kapasitiv, designet for å måle vibrasjonsforskyvning;
- I noen tilfeller (når mekanismens utforming tillater det), kan kraftsensorer også brukes til å vurdere vibrasjonsbelastningen; spesielt brukes de mye til å måle vibrasjonsbelastningen på hardlagerstøtter for balanseringsmaskiner.
Vibrasjon er altså en maskins reaksjon på ytre krefter. Størrelsen på vibrasjonen avhenger ikke bare av størrelsen på kraften som virker på mekanismen, men også av stivheten til mekanismens design. En og samme kraft kan føre til forskjellige vibrasjoner. I en maskin med harde lagre kan lagrene utsettes for betydelige dynamiske belastninger, selv om vibrasjonene er små. Derfor brukes kraftsensorer i stedet for vibrasjonssensorer (vibrasjonsakselerometre) ved avbalansering av maskiner med harde lagre.
Vibrasjonssensorer brukes på mekanismer med relativt bøyelige støtter, når virkningen av ubalanserte sentrifugalkrefter fører til en merkbar deformasjon av støttene og vibrasjoner. Kraftsensorer brukes på stive støtter, når selv betydelige krefter på grunn av ubalanse ikke fører til nevneverdig vibrasjon.
Resonans er en faktor som forhindrer balansering.
Vi har tidligere nevnt at rotorer deles inn i stive og fleksible. Rotorens stivhet eller fleksibilitet må ikke forveksles med stivheten eller bevegeligheten til støttene (fundamentet) som rotoren er montert på. En rotor regnes som stiv når dens deformasjon (bøying) under påvirkning av sentrifugalkreftene kan neglisjeres. Deformasjonen av en fleksibel rotor er relativt stor og kan ikke neglisjeres.
I denne artikkelen tar vi kun for oss balansering av stive rotorer. En stiv (ikke-deformerbar) rotor kan i sin tur være montert på stive eller bevegelige (bøyelige) støtter. Det er klart at denne stivheten/bevegeligheten til støttene også er relativ, avhengig av rotorhastigheten og størrelsen på de resulterende sentrifugalkreftene. En betinget grense er frekvensen på egenvibrasjonene til rotorstøttene.
For mekaniske systemer bestemmes formen og frekvensen til egenvibrasjonene av massen og elastisiteten til elementene i det mekaniske systemet. Det vil si at frekvensen av naturlige vibrasjoner er en intern egenskap ved det mekaniske systemet og ikke avhenger av ytre krefter. Når de blir avbøyd fra likevektstilstanden, har støtter på grunn av elastisitet en tendens til å gå tilbake til likevektsposisjonen. Men på grunn av den massive rotorens treghet har denne prosessen karakter av dempede svingninger. Disse vibrasjonene er de naturlige vibrasjonene i rotor-støttesystemet. Frekvensen avhenger av forholdet mellom rotorens masse og støttenes elastisitet.
Når rotoren begynner å rotere og rotasjonsfrekvensen nærmer seg frekvensen for naturlige vibrasjoner, øker vibrasjonsamplituden kraftig, noe som kan føre til ødeleggelse av strukturen.
Fenomenet mekanisk resonans oppstår. I resonansområdet kan en endring av rotasjonshastigheten med 100 o/min føre til at vibrasjonene øker flere titalls ganger. Samtidig (i resonansområdet) endres vibrasjonsfasen med 180°.
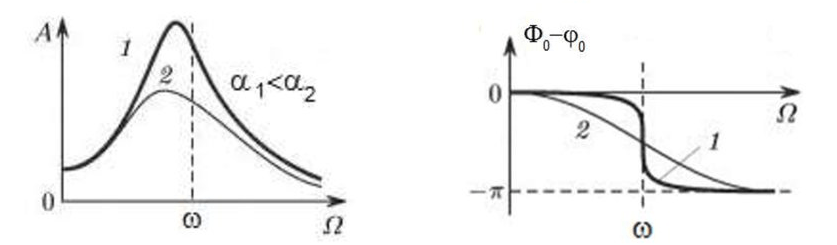
Hvis utformingen av mekanismen ikke lykkes og driftsfrekvensen til rotoren er nær frekvensen av naturlige vibrasjoner, da blir driften av mekanismen umulig på grunn av den uakseptabelt høye vibrasjonen. Dette er ikke mulig på vanlig måte, siden selv en liten hastighetsendring vil føre til en drastisk endring i vibrasjonsparametrene. For balansering i resonansområdet brukes spesielle metoder som ikke er vurdert i denne artikkelen.
Det er mulig å bestemme frekvensen til mekanismens egenvibrasjoner ved utrulling (ved utkobling av rotorrotasjonen) eller ved hjelp av støtmetoden med påfølgende spektralanalyse av systemets respons på støtet.
For mekanismer med en rotasjonsfrekvens som ligger over resonansfrekvensen, dvs. som arbeider i resonansmodus, anses støttene å være i bevegelse, og til måling brukes vibrasjonssensorer, hovedsakelig vibroacelerometre, som måler akselerasjonen til strukturelementene. For mekanismer som opererer i preresonant modus, anses støttene som stive. I dette tilfellet brukes kraftsensorer.
Lineære og ikke-lineære modeller av et mekanisk system. Ikke-linearitet er en faktor som gjør det umulig å balansere
Ved balansering av stive rotorer brukes matematiske modeller, såkalte lineære modeller, til balanseringsberegninger. En lineær modell betyr at i en slik modell er den ene størrelsen proporsjonal (lineær) med den andre. Hvis for eksempel den ukompenserte massen på rotoren dobles, vil vibrasjonsverdien også dobles. For stive rotorer kan en lineær modell brukes, siden de ikke deformeres.
For fleksible rotorer kan den lineære modellen ikke lenger brukes. For en fleksibel rotor, hvis massen til det tunge punktet øker under rotasjon, vil det oppstå ytterligere deformasjon, og i tillegg til massen vil også radiusen til plasseringen av det tunge punktet øke. For en fleksibel rotor vil derfor vibrasjonen øke mer enn to ganger, og de vanlige beregningsmetodene vil ikke fungere.
Også endringen av elastisiteten til støtter ved deres store deformasjoner, for eksempel når noen strukturelle elementer fungerer ved små deformasjoner av støtter, og ved store er andre strukturelle elementer involvert. Dette er grunnen til at du ikke kan balansere mekanismer som ikke er festet på et fundament, men for eksempel bare plassert på gulvet. Ved betydelige vibrasjoner kan kraften fra ubalansen trekke mekanismen opp fra gulvet, og dermed endre systemets stivhetsegenskaper betydelig. Motorføttene må være godt festet, boltefestene må være godt strammet, tykkelsen på underlagsskivene må gi tilstrekkelig stivhet osv. Hvis lagrene er ødelagte, er det fare for betydelig feilinnretting av akselen og støt, noe som også vil føre til dårlig linearitet og manglende evne til å utføre en kvalitetsbalanse.
Balanseringsinnretninger og balanseringsmaskiner
Som nevnt ovenfor er balansering prosessen med å justere den viktigste sentrale treghetsaksen med rotorens rotasjonsakse.
Denne prosessen kan utføres på to måter.
Den første metoden går ut på å bearbeide rotortappene på en slik måte at aksen som går gjennom midten av tappene, krysser rotorens sentrale treghetsakse. En slik teknikk brukes sjelden i praksis og vil ikke bli diskutert i detalj i denne artikkelen.
Den andre (vanligste) metoden innebærer å flytte, installere eller fjerne korreksjonsvekter på rotoren, som plasseres slik at rotorens treghetsakse ligger så nær rotasjonsaksen som mulig.
Flytting, tilsetning eller fjerning av korreksjonsvekter under balansering kan gjøres ved hjelp av ulike teknologiske operasjoner, blant annet boring, fresing, overflatebehandling, sveising, skruing eller avskruing, laser- eller elektronstrålebrenning, elektrolyse, elektromagnetisk overflatebehandling osv.
Balanseringsprosessen kan utføres på to måter:
- balansering av monterte rotorer (i egne lagre) ved hjelp av balanseringsmaskiner;
- balansering av rotorer på balanseringsmaskiner. For balansering av rotorer i egne lagre brukes vanligvis spesialiserte balanseringsenheter (sett), som gjør det mulig å måle vibrasjonen til den balanserte rotoren ved dens rotasjonsfrekvens i vektorform, dvs. å måle både amplituden og fasen av vibrasjonen. I dag produseres de ovennevnte enhetene på grunnlag av mikroprosessorteknologi og (i tillegg til vibrasjonsmåling og -analyse) gir de automatisk beregning av parametere for korrigerende vekter som bør installeres på rotoren for å kompensere for ubalansen.
Disse enhetene inkluderer:
- en måle- og beregningsenhet basert på en datamaskin eller industrikontroller;
- To (eller flere) vibrasjonssensorer;
- En fasevinkelsensor;
- tilbehør for montering av sensorene på stedet;
- spesialisert programvare som er utviklet for å utføre en full syklus med måling av rotorvibrasjonsparametere i ett, to eller flere korreksjonsplan.
To typer balanseringsmaskiner er for tiden de vanligste:
- Mykbæringsmaskiner (med myke støtter);
- Maskiner med harde lagre (med stive støtter).
Maskiner med myke lagre har relativt bøyelige støtter, for eksempel basert på flate fjærer. Frekvensen av naturlige vibrasjoner i disse støttene er vanligvis 2-3 ganger lavere enn rotasjonsfrekvensen til balanseringsrotoren, som er montert på dem. Vibrasjonssensorer (akselerometre, vibrasjonshastighetssensorer, etc.) brukes vanligvis når man måler vibrasjonen i maskinens preresonante støtter.
Maskiner som balanserer førresonans, bruker relativt stive støtter, hvis egenvibrasjonsfrekvenser bør være 2-3 ganger høyere enn rotasjonsfrekvensen til rotoren som balanseres. Kraftgivere brukes vanligvis til å måle vibrasjonsbelastningen på maskinens støtter.
Fordelen med pre-resonansbalanseringsmaskiner er at balansering på dem kan utføres ved relativt lave rotorhastigheter (opptil 400–500 o/min), noe som forenkler utformingen av maskinen og fundamentet betraktelig, og øker produktiviteten og sikkerheten ved balansering.
Balansering av stive rotorer
Viktig!
- Balansering eliminerer kun vibrasjoner som skyldes asymmetrisk fordeling av rotormassen i forhold til rotasjonsaksen. Andre typer vibrasjoner elimineres ikke ved balansering!
- Tekniske mekanismer, hvis design sikrer fravær av resonanser ved driftsfrekvensen for rotasjon, pålitelig festet på fundamentet, installert i brukbare lagre, er gjenstand for balansering.
- Defekte maskiner må repareres før balansering. Ellers er det ikke mulig å oppnå kvalitetsbalansering.
Balansering er ingen erstatning for reparasjon!
Hovedoppgaven ved balansering er å finne massen og plasseringen av kompenserende vekter som utsettes for balanserende sentrifugalkrefter.
Som nevnt ovenfor er det som regel nødvendig og tilstrekkelig å installere to kompensasjonsvekter for stive rotorer. Dette vil eliminere både statisk og dynamisk ubalanse i rotoren. Det generelle skjemaet for måling av vibrasjoner under balansering er som følger.
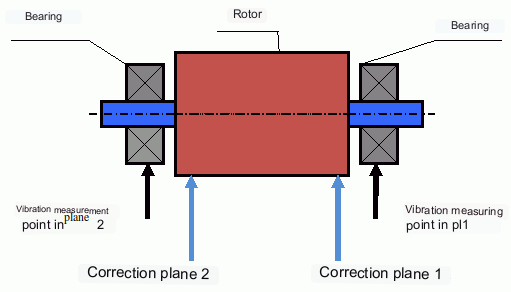
Vibrasjonssensorer er montert på lagerstøttene i punkt 1 og 2. En omdreiningsmarkør er festet til rotoren, vanligvis med reflekterende tape. RPM-merket brukes av laserturtelleren til å bestemme rotorhastigheten og fasen til vibrasjonssignalet.
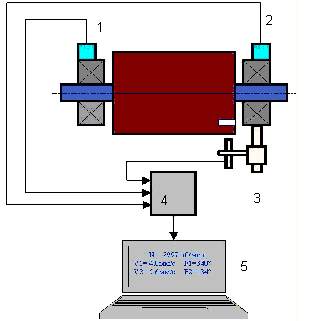
Hvordan dynamisk balansering utføres (tre-run-metoden)
I de fleste tilfeller utføres dynamisk balansering ved hjelp av metoden med tre starter. Metoden er basert på at testvekter med kjent vekt plasseres på rotoren i serie i plan 1 og 2, og vektene og plasseringen av balanseringsvektene beregnes basert på resultatene av endringer i vibrasjonsparametrene.
Plasseringen av vektene kalles korreksjonsplanet. Vanligvis velges korreksjonsplanene i området rundt lagerstøttene som rotoren er montert på.
Ved første oppstart måles den innledende vibrasjonen. Deretter plasseres en testvekt med kjent vekt på rotoren nærmere et av lagrene. En ny oppstart utføres, og vibrasjonsparametrene måles, som bør endres på grunn av testvektinstallasjonen. Deretter fjernes testvekten i det første planet og installeres i det andre planet. En tredje testkjøring utføres, og vibrasjonsparametrene måles. Testvekten fjernes, og programvaren beregner automatisk massene og installasjonsvinklene til balansevektene.
Poenget med å installere testvektene er å finne ut hvordan systemet reagerer på endringer i ubalansen. Vektene og plasseringen av testvektene er kjent, slik at programvaren kan beregne såkalte påvirkningskoeffisienter som viser hvordan en kjent ubalanse påvirker vibrasjonsparametrene. Påvirkningskoeffisientene er egenskaper ved selve det mekaniske systemet og avhenger av stivheten til støttene og massen (tregheten) til rotorstøttesystemet.
For samme type mekanismer med samme design vil påvirkningskoeffisientene ligge nær hverandre. Det er mulig å lagre koeffisientene i datamaskinens minne og bruke dem til balansering av mekanismer av samme type uten testkjøringer, noe som øker produktiviteten ved balansering betydelig. Merk at massen på testvektene bør velges slik at vibrasjonsparametrene endres merkbart når testvektene monteres. I motsatt fall øker feilen i beregningen av påvirkningskoeffisientene, og kvaliteten på balanseringen blir dårligere.
Som det fremgår av fig. 1, virker sentrifugalkraften i radial retning, dvs. vinkelrett på rotoraksen. Derfor må vibrasjonssensorene installeres slik at deres følsomhetsakse også peker i radial retning. Vanligvis er stivheten til fundamentet i horisontal retning mindre, slik at vibrasjonene i horisontal retning er høyere. For å øke følsomheten bør sensorene derfor installeres slik at følsomhetsaksen også peker i horisontal retning. Selv om det ikke er noen grunnleggende forskjell. I tillegg til vibrasjoner i radial retning må også vibrasjoner i aksial retning, langs rotorens rotasjonsakse, overvåkes. Denne vibrasjonen er vanligvis ikke forårsaket av ubalanse, men av andre årsaker, hovedsakelig relatert til feiljustering og feiljustering av akslene som er koblet sammen gjennom koblingen.
Denne vibrasjonen kan ikke elimineres ved balansering, og i så fall er det nødvendig med justering. I praksis har slike maskiner vanligvis både rotorubalanse og akselfeiljustering, noe som gjør oppgaven med å eliminere vibrasjoner mye vanskeligere. I slike tilfeller er det nødvendig å sentrere maskinen først og deretter balansere den. (Men ved sterk momentubalanse oppstår det også vibrasjon i aksial retning på grunn av "vridning" av fundamentstrukturen.)
Relaterte artikler (eksempler på balanseringsstativer)
- Balanserende stativ med myk støtte
- Balansering av rotorene til elektriske motorer
- Enkle, men effektive balansestativer
Kriterier for vurdering av kvaliteten på balanseringsmekanismer
Balanseringskvaliteten til rotorer (mekanismer) kan evalueres på to måter. Den første metoden går ut på å sammenligne størrelsen på den gjenværende ubalansen som bestemmes under balanseringsprosessen, med toleransen for gjenværende ubalanse. Disse toleransene for de ulike rotorklassene er spesifisert i ISO 1940-1-2007. Del 1. Definisjon av tillatt ubalanse.
Overholdelse av de spesifiserte toleransene kan imidlertid ikke fullt ut garantere mekanismens driftssikkerhet, knyttet til oppnåelse av minimumsnivået for vibrasjon. Dette skyldes at størrelsen på mekanismens vibrasjoner ikke bare bestemmes av størrelsen på kraften som er forbundet med den gjenværende ubalansen i rotoren, men også avhenger av flere andre parametere, inkludert: stivheten k til mekanismens strukturelle elementer, massen m, dempningsfaktoren, samt rotasjonsfrekvensen. For å estimere mekanismens dynamiske egenskaper (inkludert kvaliteten på balansen) anbefales det derfor i en rekke tilfeller å estimere mekanismens restvibrasjonsnivå, som er regulert av en rekke standarder.
Den vanligste standarden som regulerer de tillatte vibrasjonsnivåene for mekanismer, er ISO 10816-3-2002. Med hjelpen er det mulig å sette toleranser for alle typer maskiner, med tanke på kraften til deres elektriske stasjon.
I tillegg til denne universelle standarden finnes det en rekke spesialiserte standarder som er utviklet for spesifikke maskintyper. For eksempel 31350-2007 , ISO 7919-1-2002 osv.
Standarder og referanser
- ISO 1940-1:2007. Vibrasjon. Krav til balanseringskvaliteten til stive rotorer. Del 1. Bestemmelse av tillatt ubalanse.
- ISO 10816-3:2009. Mekanisk vibrasjon – Evaluering av maskinvibrasjon ved målinger på ikke-roterende deler – Del 3: Industrimaskiner med nominell effekt over 15 kW og nominelle hastigheter mellom 120 o/min og 15 000 o/min ved måling in situ.
- ISO 14694:2003. Industrivifter – Spesifikasjoner for balansekvalitet og vibrasjonsnivåer.
- ISO 7919-1:2002. Vibrasjon i maskiner uten frem- og tilbakegående bevegelse – Målinger på roterende aksler og evalueringskriterier – Generell veiledning.
VANLIGE SPØRSMÅL
Fjerner balansering all vibrasjon?
Nei. Balansering fjerner vibrasjoner forårsaket av den asymmetriske fordelingen av rotormasse i forhold til rotasjonsaksen. Vibrasjoner fra feiljustering, lagerfeil, aerodynamiske/hydrodynamiske krefter, elektromagnetiske krefter og andre årsaker krever separat diagnostikk og korrigerende tiltak.
Hvorfor kan balansering svikte nær resonans?
Nær resonans kan små hastighetsendringer forårsake store endringer i vibrasjonsamplitude og et faseskift på 180°. Under slike forhold blir måleresultatene ustabile, og konvensjonelle balanseringsprosedyrer kan ikke konvergere uten spesielle metoder.
Når trenger du balansering i ett plan kontra to plan?
For en stiv rotor er to vekter atskilt langs rotorlengden vanligvis nødvendige og tilstrekkelige for å eliminere kombinert statisk og dynamisk ubalanse. Smale rotorer viser ofte for det meste statisk ubalanse, men deformasjon og geometri kan introdusere en dynamisk komponent som kan kreve toplanskorreksjon.
Hva bør gjøres før balansering?
Sørg for at maskinen er brukbar: pålitelig montering til fundamentet, sunne lagre, ingen alvorlig løshet og ingen åpenbare kilder til ikke-linearitet. Balansering er ikke en erstatning for reparasjon.
Viktige konklusjoner
- Balansering korrigerer masserelatert (sentrifugal) eksitasjon; den løser ikke feiljustering, lagerskader eller elektromagnetiske/aerodynamiske kilder.
- Resonans og ikke-linearitet kan gjøre konvensjonell balansering ineffektiv eller usikker.
- For stive rotorer er toplansbalansering den generelle løsningen for kombinert statisk + dynamisk ubalanse.






